AVL tree

algorithms, javascript

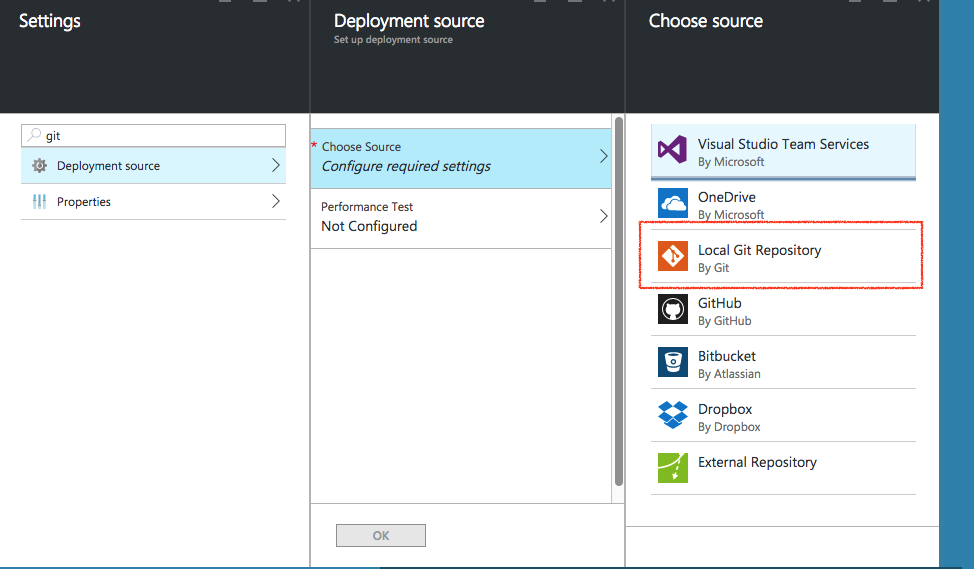
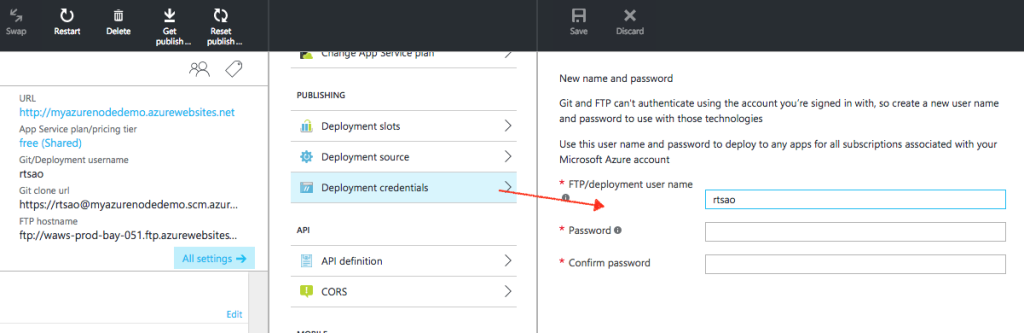
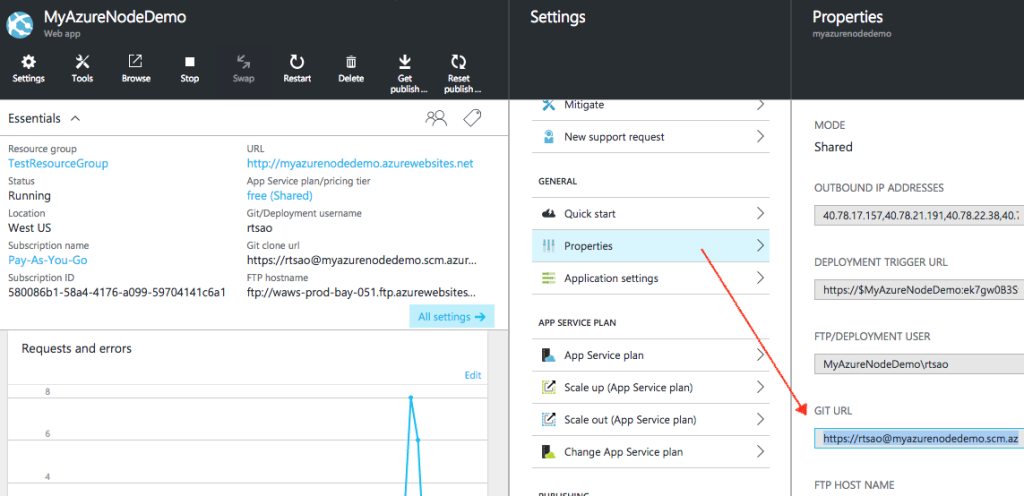
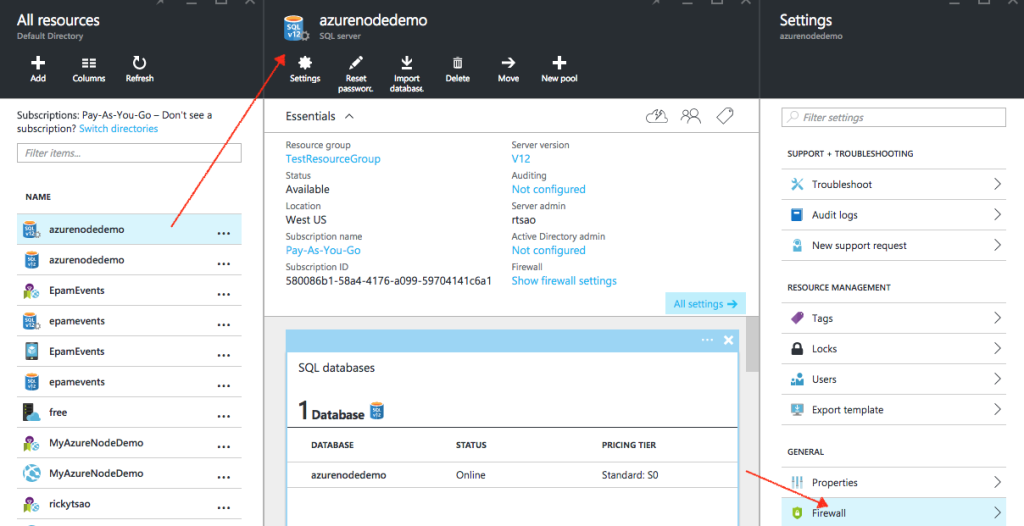
ref and source – https://github.com/redmacdev1988/avl-binary-tree

Balanced and UnBalanced Trees

height(left) – height(right) <= 1

  • Perfect tree – triangle. Height of every node is 0
  • Right skewed tree – nodes have right childs only
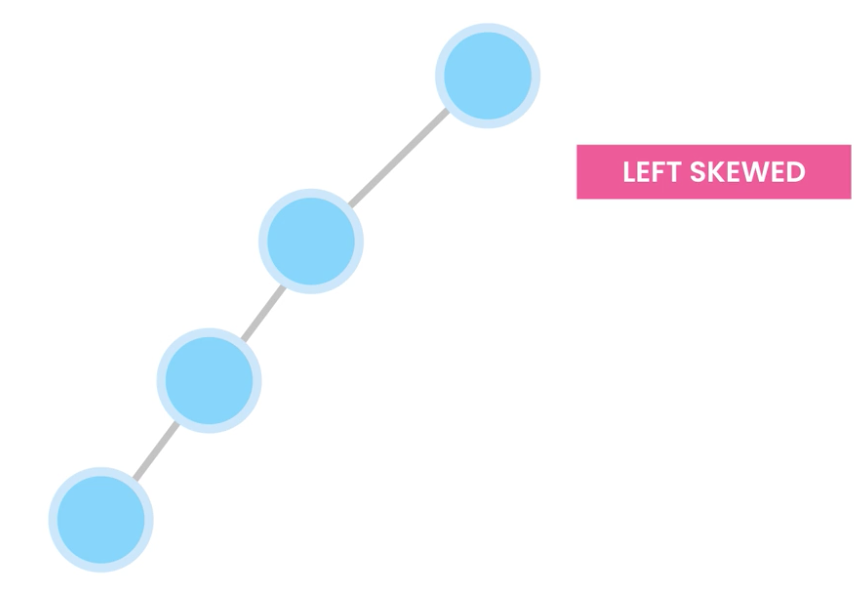
  • Left skewed tree – nodes have left childs only

It becomes a linked list and the run time back to O(n).

so…how should we add to BST so that it is more balanced?

AVL (Adelson-Velsky and Landis) is a special BST where it has self-balancing properties. There are other popular trees that also self-balances, such as red-black trees, 2-3 trees, b-trees…etc.

If distance > 1, use rotation to re-balance itself.

4 types of rotation:
Left (LL)
Right(RR)
Left-Right (LR)
Right-Left (RL

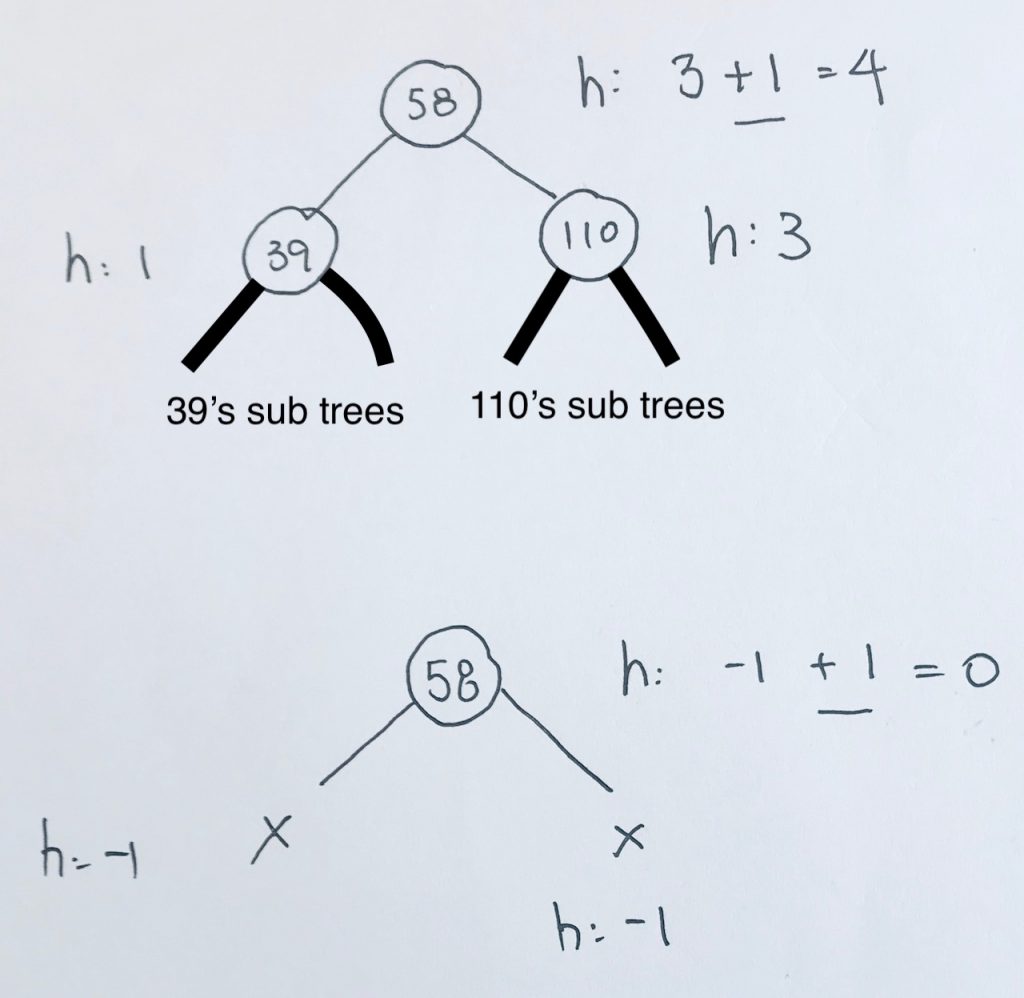
height and balance

The height of a node is the maximum number of vertices from the leaf to itself. Note thath height always start from the ground.

Thus, a leaf has a height of 0.

If the leaf has a parent node, the parent node’s height would be 1.

The balance factor of a node is the height of the left subtree minus the height of the right subtree.

  • If the result is > 0, the left subtree is larger
  • If the result is < 0, the right subtree is larger

In our example, we use absolute value as we don’t care which side is larger. We simply want to see what the balance factor is.

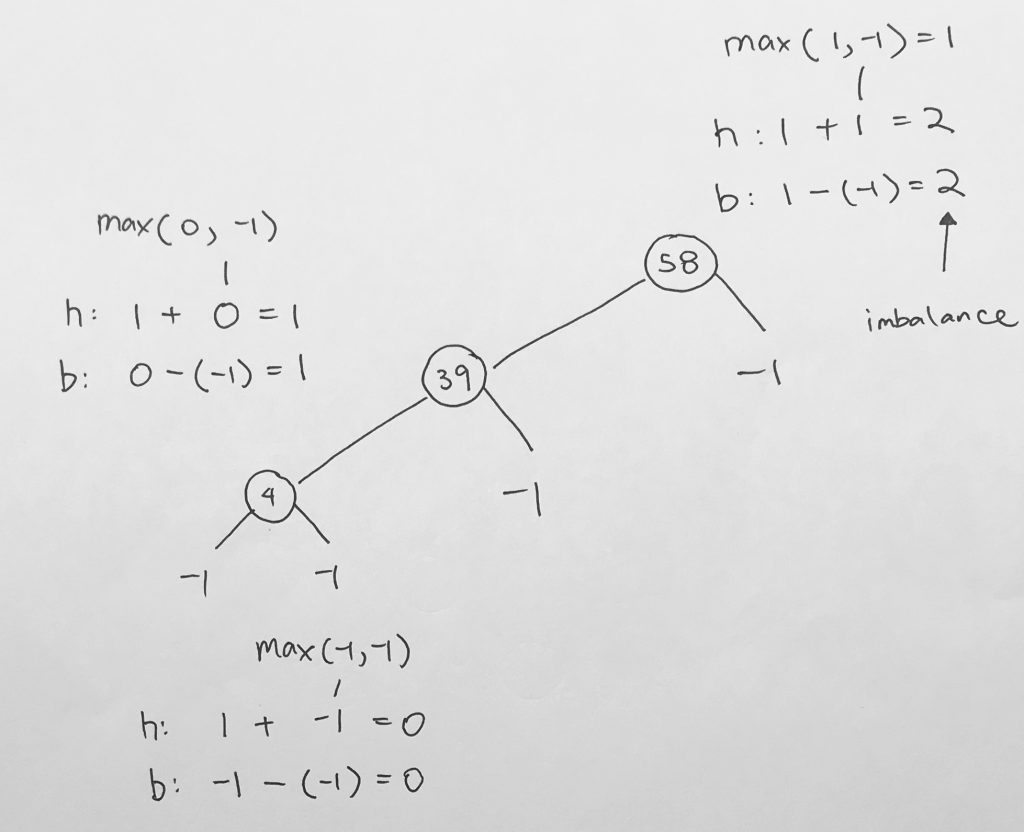
simple example

We have a root node 5, and its left node of value 2.

We calculate from the leaf. 2 is a leaf, so its height is 0. And in turn, balance factor is 0.
The left and right of a leaf is always null, thus, we don’t add 1.

At 5, the height is calculated as height of the subtree + 1. Thus, we get 1 for left subtree. And obviously 0 for right subtree. The height is the max of those 2 numbers. We get 1. The balance is the difference in the height of the left and right subtree, which is 1.

In the next example, it is the same, but simply flipped. The leaf has height of 0 because there is no left or right subtrees. Thus, its balance is also 0.
The root node 8’s left subtree is null, so its height is defaulted to 0.
Its right subtree exists so we add 1 to right subtree height (0), which results to 1.

Our balance is abs value of (left height – right height), which is abs(0-1) = 1.

In the last example, 50 is the root. Its left subtree is 10, which has height of 0, balance of 0.
Its right subtree is 80 which has height of 0, balance of 0.

Thus, at 50, its left height is 0 + 1. right height is 0 + 1, thus, max of left and right height is 1.
Its balance is therefore abs(1 – 1) = 0

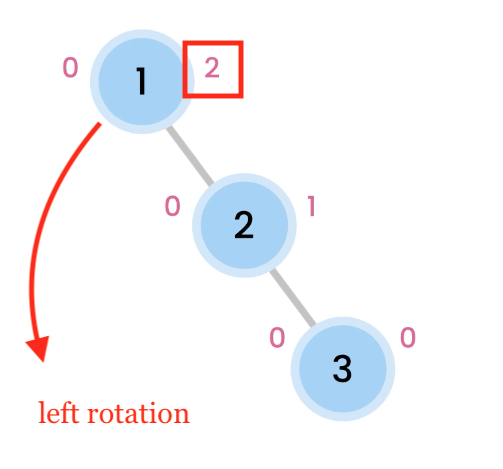
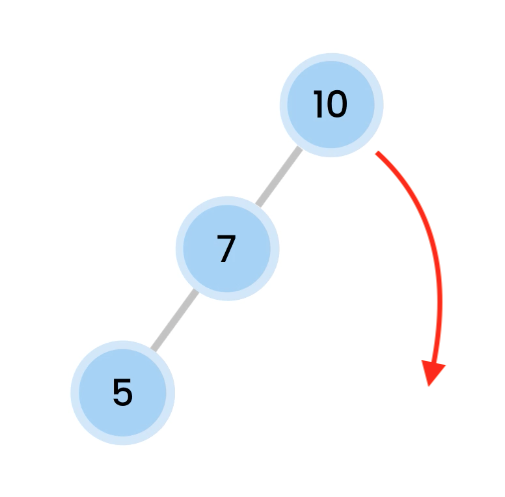
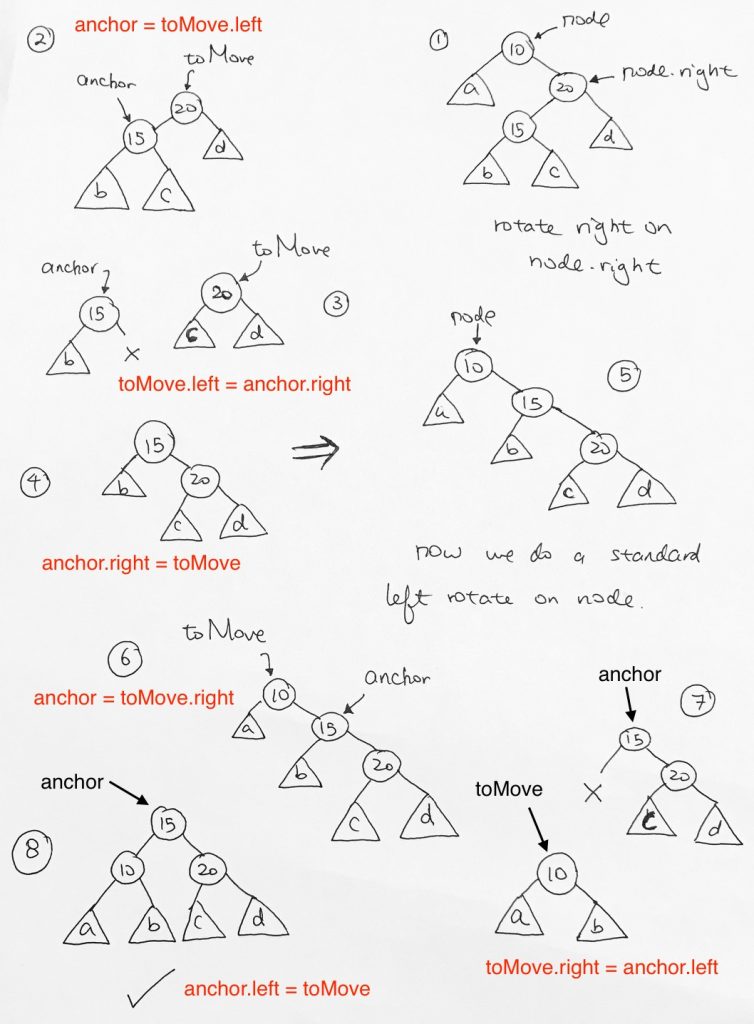
Left Rotation

Right skewed trees are rebalanced by doing a Left Rotation.

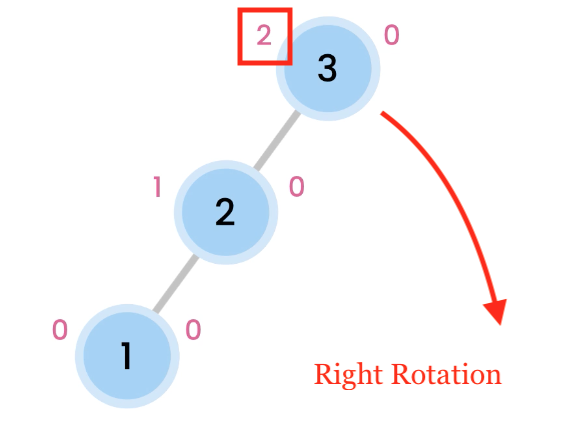
Right Rotation

Left skewed trees are rebalanced by doing a Right Rotation.

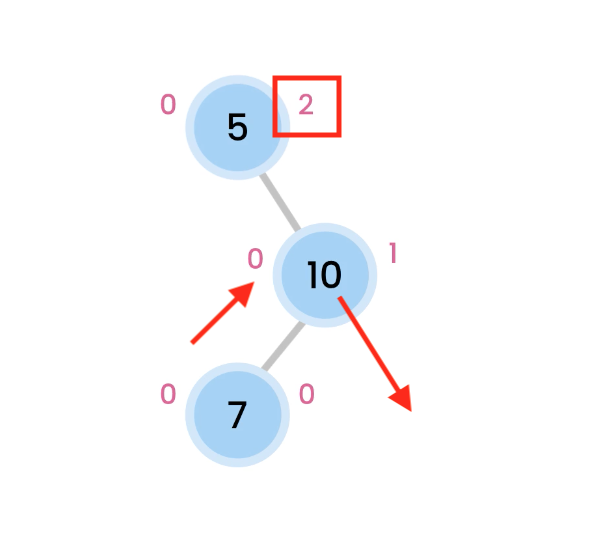
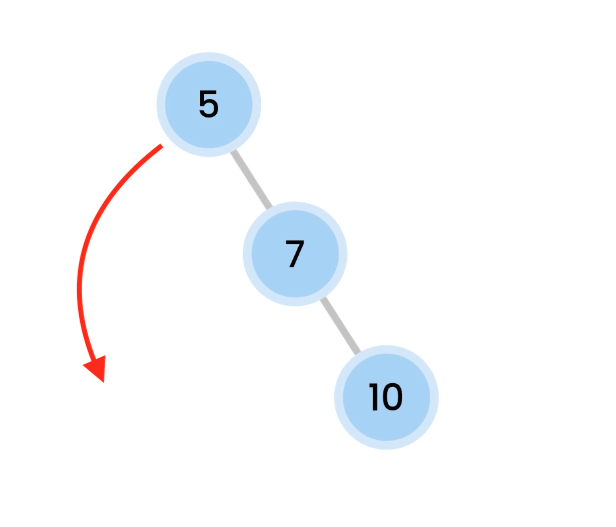
Left Right Rotation

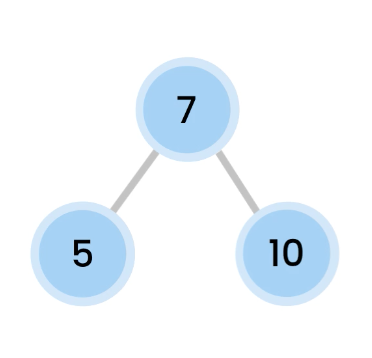
Left rotation on 5, so 7 comes up.

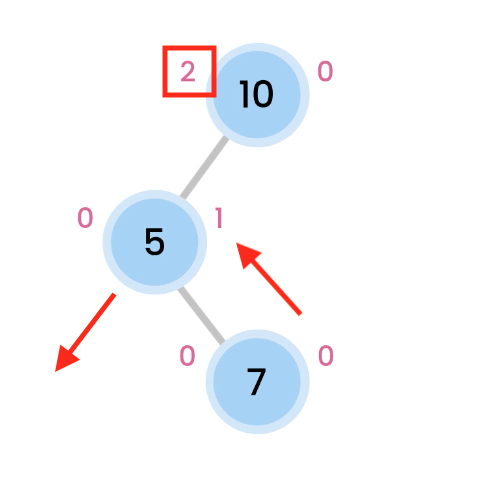
then we do a Right rotation, which makes 10 comes down.

And now, we are balanced.

Left Right Rotation

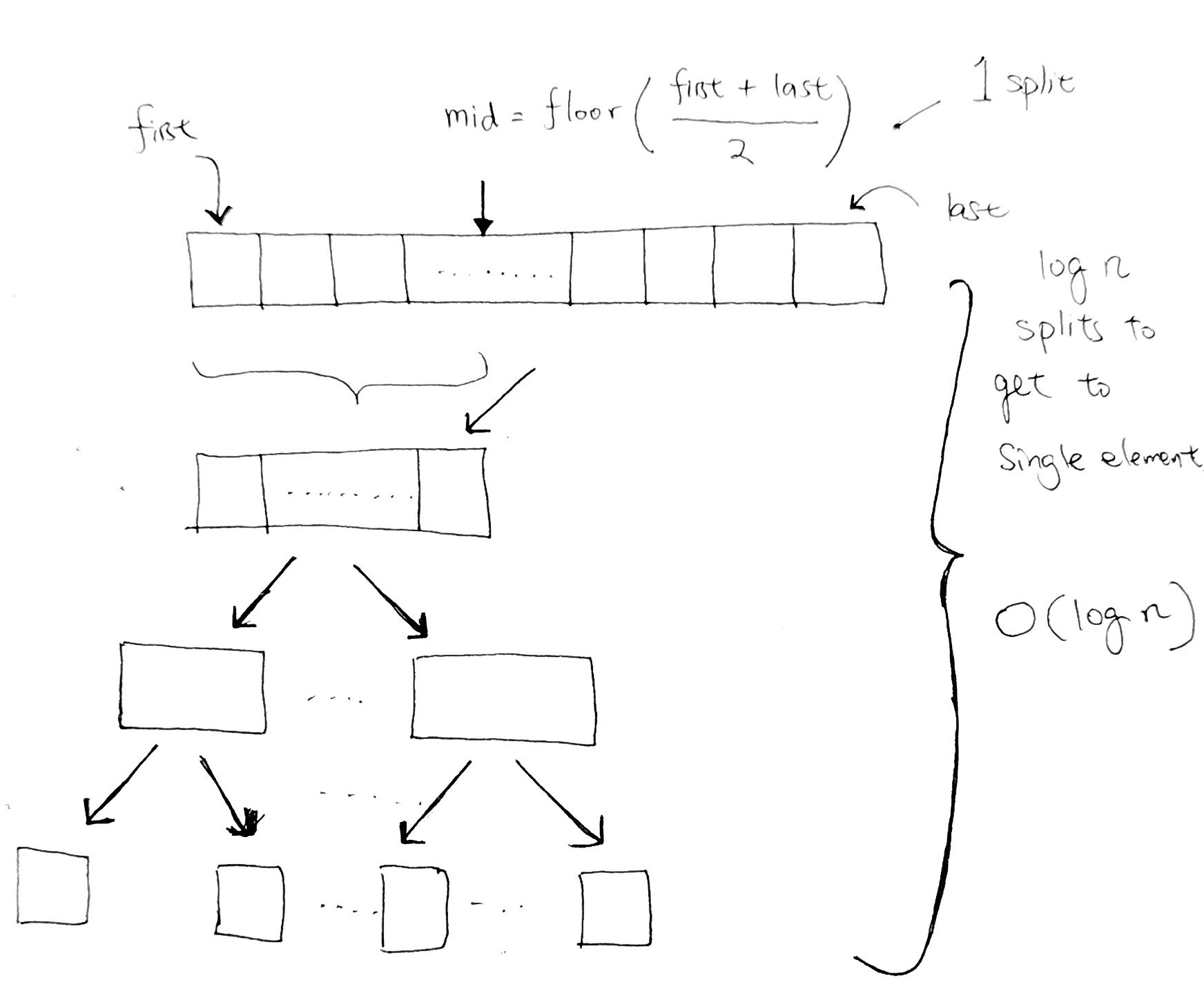
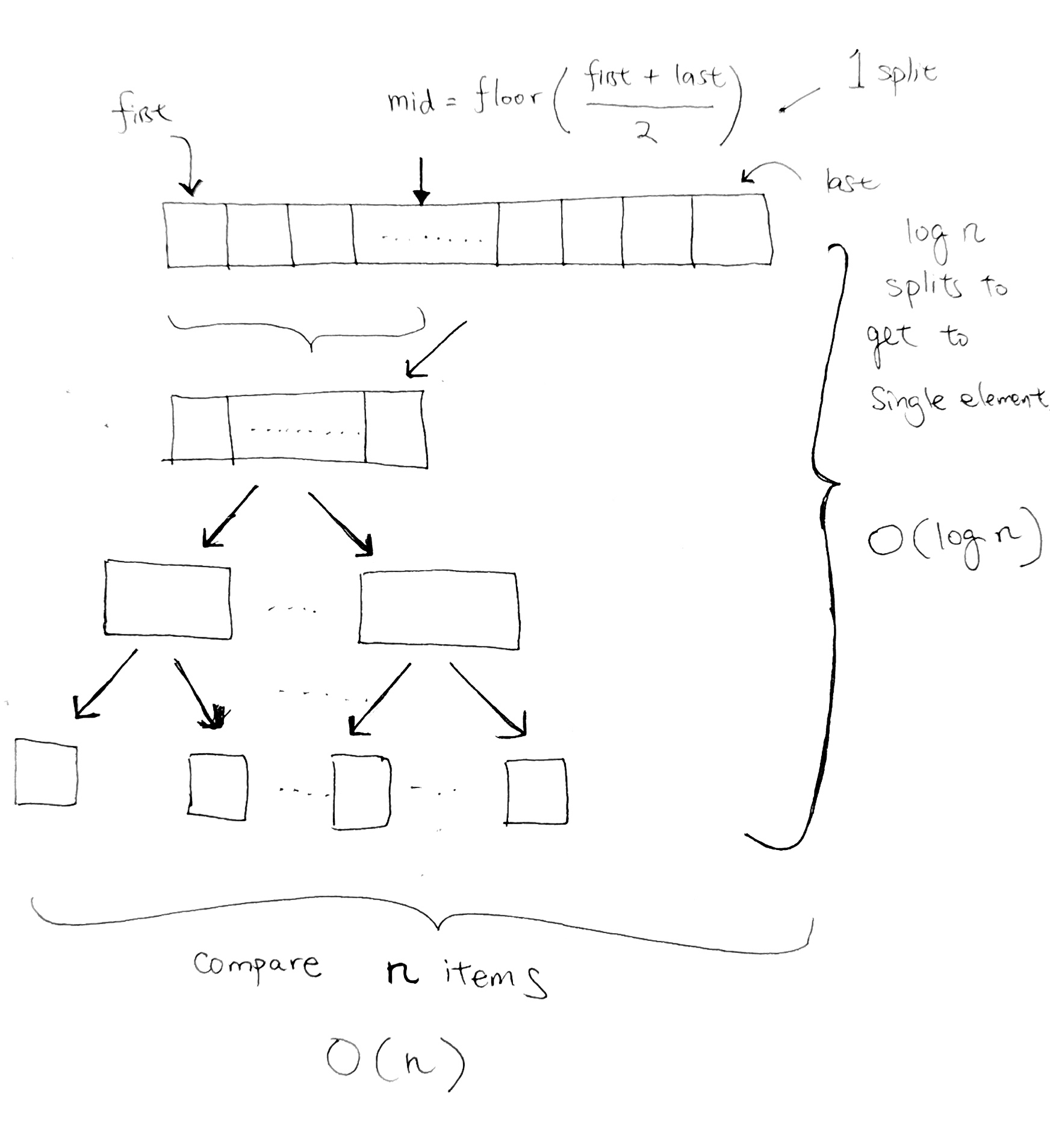
Height Calculations

After inserting new node into an AVL tree, we must re-calculate every node’s height.

code for UPDATE of height and balance

The code shows, if we’re at a subtree that is null, we don’t add 1. If there exists a subtree, we add 1 to the height of that subtree in order to get our current height.

We do this for both left and right.

The balance is simply the difference between the heights.

balanceFactor = height(L) – height(R)
> 1 => left heavy, perform right rotation
< -1 right heavy, perform left rotation

more examples

/ rotation

< rotation

> rotation

\ rotation

In order to fix it, we must do a left rotation.

Insertion with Balance

Removal of Node

Removal of Node is straightforward. We use public function remove and it uses utility traverseRemove function. travereRemove traverses the tree until it gets to the node with the value you want to remove.

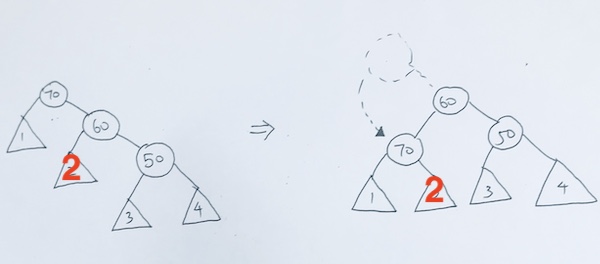
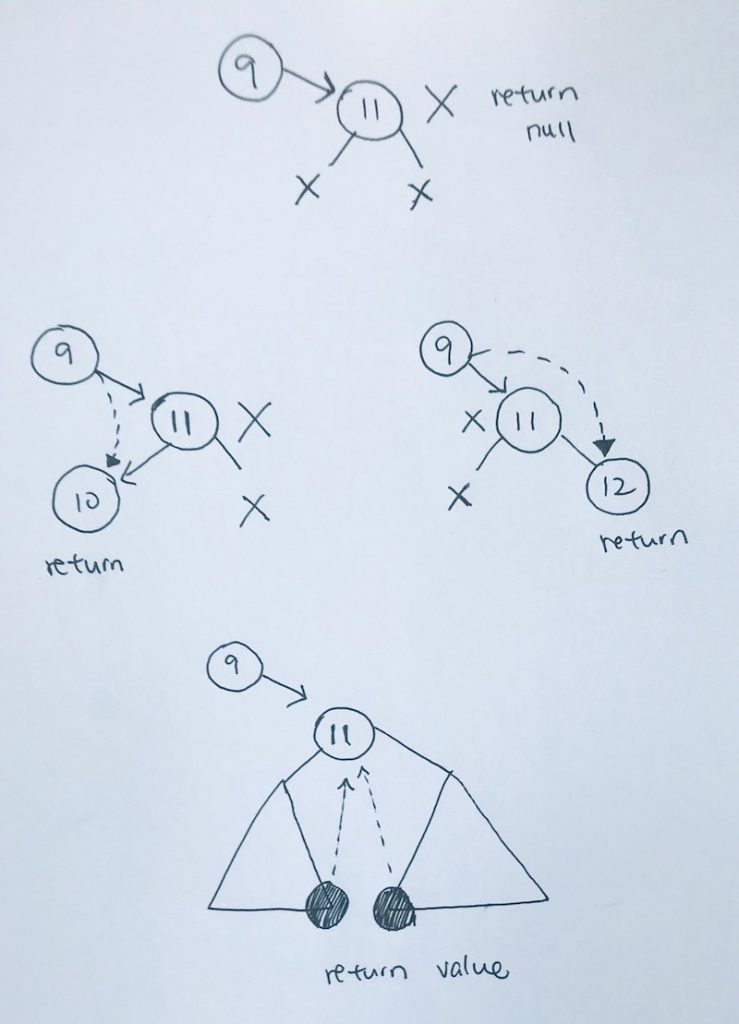
When we find the node we’re looking for, it will look at 4 situations:

1) no children, simply delete and remove the current node
2) only the left child exist, so we return the node’s left subtree to be attached. remove the node
3) only the right child exist, so we return the node’s right subtree to be attached. remove the node.

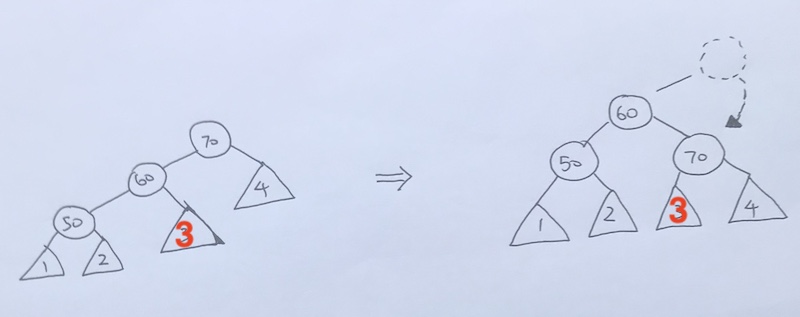
4) both child exist.

This is the key in deletion. In this particular case, we want to return the leftmost of the right subtree or rightmost of the left subtree.
In our example, we return the leftmost of the rightsubtree.

ref – https://github.com/redmacdev1988/avl-binary-tree

Binary Search Tree

algorithms, C/C++/Objective-C

http://code.runnable.com/VUTjJDME6nRv_HOe/delete-node-from-bst-for-c%2B%2B

demo download xCode 7.3 (c++)

Adding to Tree Concept

Traverse until you hit a leaf. Then, Re-point at the leaf

Finding from Tree Concept

Traverse if data does not match. If at leaf, return NULL.

1) we need the node back, hence, we return our traversals.
2) When we find our target node, we return a new Node with that value. That return will return traverse back.
3) If nothing is found then we return NULL.

Running Time

Average Time

Access: O(log(n))
Search: O(log(n))
Insertion: O(log(n))
Deletion: O(log(n))

Worst Time (due to unbalanced tree that deteriorates to a linear tree

Access: O(n)
Search: O(n)
Insertion: O(n)
Deletion: O(n)

The Node – building block of the Binary Search Tree

First we must create the building block of the tree. It is an object with a data container, a left pointer, and right pointer. Each pointer denotes a leaf.

You can initialize this object by value, and set both leafs to NULL.
Or you can pass in data to set everything.

Creating a BST tree

First we create the BST class. The key thing here is to add a private member for the root Node. This is the starting point of all tree manipulations.
Then we add the void addNode(Node * root, int newVal) for adding data algorithm.

Adding Nodes O(log n)

We start at the root node, and check the value of it with the incoming new value.

If the new value is larger than the root, then:

1) If the right node exist, we move down the right side of the tree via recursion.
2) If the right node is NULL, we create a new Node, and point it to the right node.

If the new value is smaller or equal than the root, then:

1) If the left node exist, we move down the left side of the tree via recursion.
2) If the left node is NULL, we create a new Node, and point it to the left node.

http://stackoverflow.com/questions/9456937/when-to-use-preorder-postorder-and-inorder-binary-search-tree-traversal-strate

Depth First Search – Pre order (left side)

print
recursion left
recursion right

If you know you need to explore the roots before inspecting any leaves, you pick pre-order because you will encounter all the roots before all of the leaves.

Depth First Search – Post order (right side)

recursion left
recursion right
print

If you know you need to explore all the leaves before any nodes, you select post-order because you don’t waste any time inspecting roots in search for leaves.

Depth First Search – In order (bottom side)

recursion left
print
recursion right

If you know that the tree has an inherent sequence in the nodes, and you want to flatten the tree back into its original sequence, than an in-order traversal should be used. The tree would be flattened in the same way it was created. A pre-order or post-order traversal might not unwind the tree back into the sequence which was used to create it.

Search for a value O(log n)

Search a value in the binary tree is the fastest. The time is O(log n).

If the node is not NULL, we recursively go down the tree according to if the “to get” value is larger or smaller. Then when we hit a node value that matches, we just return the current node.

Deletion O(log n)

Deletion is O(log n + k).

Delete All Nodes

The idea behind deleting all the nodes is a thorough recursion through the left and right.

We delete in 2 situations:

1) delete the node if it has no children
2) delete the node after left and right recursion.

given that if a root is NULL, we just return.
If a node has one child (and the other is NULL), then the NULL leaf just returns.
We recurse down the child.

BST.cpp

Testing it all

idempotent for PUT vs POST

HTML

http://stackoverflow.com/questions/630453/put-vs-post-in-rest?rq=1

Better is to choose between PUT and POST based on idempotence of the action.

PUT implies putting a resource – completely replacing whatever is available at the given URL with a different thing. By definition, a PUT is idempotent. Do it as many times as you like, and the result is the same.

x = 5 is idempotent. You can PUT a resource whether it previously exists, or not (eg, to Create, or to Update)!

POST updates a resource, adds a subsidiary resource, or causes a change. A POST is not idempotent, in the way that x++ is not idempotent.

By this argument, PUT is for creating when you know the URL of the thing you will create. POST can be used to create when you know the URL of the “factory” or manager for the category of things you want to create.

so:

POST /expense-report
or:

PUT /expense-report/10929

about Json Web Tokens (JWT)

Node JS

todo –
https://www.freecodecamp.org/news/securing-node-js-restful-apis-with-json-web-tokens-9f811a92bb52/

https://medium.com/swlh/a-practical-guide-for-jwt-authentication-using-nodejs-and-express-d48369e7e6d4

https://scotch.io/tutorials/the-anatomy-of-a-json-web-token

The reason why JWT are used is to prove that the sent data was actually created by an authentic source.

JSON Web Tokens work across different programming languages: JWTs work in .NET, Python, Node.js, Java, PHP, Ruby, Go, JavaScript, and Haskell. So you can see that these can be used in many different scenarios.

JWTs are self-contained: They will carry all the information necessary within itself. This means that a JWT will be able to transmit basic information about itself, a payload (usually user information), and a signature.

JWTs can be passed around easily: Since JWTs are self-contained, they are perfectly used inside an HTTP header when authenticating an API. You can also pass it through the URL.

What is a JWT

Since there are 3 parts separated by a ., each section is created differently. We have the 3 parts which are:

  • header
  • payload
  • signature

header

The header carries 2 parts:

declaring the type, which is JWT
the hashing algorithm to use (HMAC SHA256 in this case)

Now once this is base64encode, we have the first part of our JSON web token!

eyJhbGciOiJIUzI1NiIsInR5cCI6IkpXVCJ9

{“alg”:”HS256″,”typ”:”JWT”} is treated as a string, which encodes to eyJhbGciOiJIUzI1NiIsInR5cCI6IkpXVCJ9

If you were to chop off some string, for example {“alg”:”HS256″,, it will encode to eyJhbGciOiJIUzI1NiIs.

What is base64encode?

http://stackoverflow.com/questions/201479/what-is-base-64-encoding-used-for

Encoding transforms data into another format using a scheme that is publicly available so that it can easily be reversed. Hence, it is for maintaining data usability and uses schemes that are publicly available.

When you have some binary data that you want to ship across a network, you generally don’t do it by just streaming the bits and bytes over the wire in a raw format.

Why?

– because some media are made for streaming text.
– some protocols may interpret your binary data as control characters (like a modem)
– your binary data could be screwed up because the underlying protocol might think that you’ve entered a special character combination

So to get around this, people encode the binary data into characters. Base64 is one of these types of encodings. Why 64? Because you can generally rely on the same 64 characters being present in many character sets, and you can be reasonably confident that your data’s going to end up on the other side of the wire uncorrupted.

How does base64 work?

https://en.wikipedia.org/wiki/Base64

Another example:

A quote from Thomas Hobbes’ Leviathan (be aware of spaces between lines):

Man is distinguished, not only by his reason, but by this singular passion from
other animals, which is a lust of the mind, that by a perseverance of delight
in the continued and indefatigable generation of knowledge, exceeds the short
vehemence of any carnal pleasure.

is represented as a byte sequence of 8-bit-padded ASCII characters encoded in MIME’s Base64 scheme as follows:

TWFuIGlzIGRpc3Rpbmd1aXNoZWQsIG5vdCBvbmx5IGJ5IGhpcyByZWFzb24sIGJ1dCBieSB0aGlz
IHNpbmd1bGFyIHBhc3Npb24gZnJvbSBvdGhlciBhbmltYWxzLCB3aGljaCBpcyBhIGx1c3Qgb2Yg
dGhlIG1pbmQsIHRoYXQgYnkgYSBwZXJzZXZlcmFuY2Ugb2YgZGVsaWdodCBpbiB0aGUgY29udGlu
dWVkIGFuZCBpbmRlZmF0aWdhYmxlIGdlbmVyYXRpb24gb2Yga25vd2xlZGdlLCBleGNlZWRzIHRo
ZSBzaG9ydCB2ZWhlbWVuY2Ugb2YgYW55IGNhcm5hbCBwbGVhc3VyZS4=

In the above quote, let’s take the example of the word ‘Man’.

How to encode ‘Man’ into ‘TWFu’

General idea:

Encoded in ASCII, the characters M, a, and n are stored as the bytes 77, 97, and 110, respectively.
They are also the 8-bit binary values 01001101, 01100001, and 01101110.

These three values are joined together into a 24-bit string, producing 010011010110000101101110.

Groups of 6 bits (6 bits have a maximum of 2 to the 6 = 64 different binary values) are converted into individual numbers from left to right (in this case, there are four numbers in a 24-bit string), which are then converted into their corresponding Base64 character values.

In detail:

Say our text content is “Man”

Originally, the 3 values in bits are:

01001101 01100001 01101110

We split this into 6 bits of 4 index integers

010011 010110 000101 101110
where
010011 –> 19
010110 –> 22
000101 –> 5
101110 –> 46

Put these integers through the Base64 index table, would give us
TWFu

Payload

The payload will carry the bulk of our JWT, also called the JWT Claims. This is where we will put the information that we want to transmit and other information about our token.

There are multiple claims that we can provide. This includes registered claim names, public claim names, and private claim names.

REGISTERED CLAIMS

Claims that are not mandatory whose names are reserved for us.

These include:

  • iss: The issuer of the token
  • sub: The subject of the token
  • aud: The audience of the token
  • exp: This will probably be the registered claim most often used. This will define the expiration in NumericDate value. The expiration MUST be after the current date/time.
  • nbf: Defines the time before which the JWT MUST NOT be accepted for processing
  • iat: The time the JWT was issued. Can be used to determine the age of the JWT
  • jti: Unique identifier for the JWT. Can be used to prevent the JWT from being replayed. This is helpful for a one time use token.

PUBLIC CLAIMS

These are the claims that we create ourselves like user name, information, and other important information.

PRIVATE CLAIMS

A producer and consumer may agree to use claim names that are private. These are subject to collision, so use them with caution.

For example

This will encode64 to:

eyJpc3MiOiJzY290Y2guaW8iLCJleHAiOjEzMDA4MTkzODAsIm5hbWUiOiJDaHJpcyBTZXZpbGxlamEiLCJhZG1pbiI6dHJ1ZX0

Signature

The third and final part of our JSON Web Token is going to be the signature. This signature is made up of a hash of the following components:

  • the header
  • the payload

    • secret

This is how we get the third part of the JWT:

The secret is the signature held by the server. This is the way that our server will be able to verify existing tokens and sign new ones.

This gives us the final part of our JWT:
03f329983b86f7d9a9f5fef85305880101d5e302afafa20154d094b229f75773

Thus, our JWT is now:

eyJhbGciOiJIUzI1NiIsInR5cCI6IkpXVCJ9.eyJpc3MiOiJzY290Y2guaW8iLCJleHAiOjEzMDA4MTkzODAsIm5hbWUiOiJDaHJpcyBTZXZpbGxlamEiLCJhZG1pbiI6dHJ1ZX0.03f329983b86f7d9a9f5fef85305880101d5e302afafa20154d094b229f75773

The JSON Web Token standard can be used across multiple languages and is quickly and easily interchangeable.

You can use the token in a URL, POST parameter, or an HTTP header. The versatility of the JSON Web Token let’s us authenticate an API quickly and easily by passing information through the token.

merge sort

algorithms

MergeSort(js)

Typescript

Part 1 – The split

Originally, we recurse into a function, along with a base case.

Printing the parameter first will count down from 3.

When we hit our terminating case of zero at (1), we return, and execution from the recursion continues downwards at (2).
As each function pops off from the stack, we log the index again. This time we go 1, 2, and finally back to 3.

Thus display is:

3 2 1 0 1 2 3

In Mergesort, the idea is that there is a total of n elements. We use splitting in half in order to cut down everything into single elements. Each cut is the same concept behind going down one level in a binary tree. We half all the elements.

In order to reach single elements, the running time is the height of the tree, or (log n) splits.

And in order to go into each halved section to split some more, we use recursion.

Let’s look at how MergeSort does this split:

in code:

The output is:

haha, hoho, hehe, hihi, alloy, Zoy

Part 2 – The Merge

Printing the words out is our first step, and we’ve used recursion. Now we need to compare each word and sort everything.

When we get to haha, we return an array with “haha”. Same with “hoho”. As we recursive back down the stack one step, we now have two arrays. We need to compare everything in these two arrays and sort them into a new array.

  1. We first create a n space ‘result’ array that is the total length of the arrays.
  2. We do this so that we will sort each element of these two arrays and put them into our result array.
  3. We do this until one of the arrays finish.
  4. Then we just tack on whatever is left from the array that still has untouched elements

Full code

Each level represents one split. And we have a total of (log n) split.
At every level, we do a comparison for every element. Thus our running time for the sort is O(n log n).

The standard merge sort on an array is not an in-place algorithm, since it requires O(N) additional space to perform the merge. During merge, we create a result array in order to carry the left and right array. This is where O(n) additional space comes from:

However, there exists variants which offer lower additional space requirement.

It is stable because it keeps the ordering intact from the input array.

Say we have [‘a’, ‘a’, ‘x’, ‘z’]. We split until we get single elements.

[‘a’, ‘a’] and [‘x’, ‘z’]

[‘a’] [‘a’] [‘x’] [‘z’]

We compare ‘a’ and ‘a’.

This is where it is stable because we always keep the 1st ‘a’ before the 2nd ‘a’ in the results array, which requires O(n) Auxiliary space, during the merge.

We place the leftmost ‘a’ first. Then we put the right side ‘a’ next into the result array.

Say we have another sample data where [‘a’, ‘z’, ‘m’,’b’, ‘a’, ‘c’] and we start recursing via mid splits:

[‘a’, ‘z’, ‘m’] [‘b’, ‘a’, ‘c’]
[‘a’, ‘z’] [‘m’] [‘b’, ‘a’] [‘c’]
[‘a’] [‘z’] [‘m’] [‘b’] [‘a’] [‘c’]

Now we star the merge process:

[‘a’, ‘z’] [‘m’] [‘a’, ‘b’] [‘c’]
[‘a’, ‘m’, ‘z’] [‘a’, ‘b’, ‘c’]

As you can see at this part, we do the final merge and because ‘a’ === ‘a’, we always insert the left-side ‘a’ inside of our results array first. Then we place the right-side ‘a’. Thus, keeping it stable.

Full Source (Typescript)

Javascript version

In-Place: The standard merge sort on an array is not an in-place algorithm, since it requires O(N) additional space to perform the merge. There exists variants which offer lower additional space requirement.

Stable: yes. It keeps the ordering intact from the input array.

http://www.codenlearn.com/2011/10/simple-merge-sort.html

Merge Sort has 2 main parts. The 1st part is the double recursion. The 2nd part is the Merge itself.

1) double recursion

2 recursion calls is executed, one after the other. Usually, in a single recursion, we draw a stack with the recursion and its parameter, and calculate it that way.

However, with two recursions, we simply have more content on the stack in our drawing.

For example, say we have an array of integers, with index 0 to 10.

mergeSort says:

So we call mergeSort recursively twice, with different parameters. The way to cleanly calculate them is to
write out the parameters, see if the left < right condition holds. If it does, then write result for the 'center' variable. Evaluate the 2 mergeSort calls and the merge Call. You will then clearly see the order of execution:

Let’s take a look at how the cursive call operates

Say we have [‘a’, ‘b’, ‘c’, ‘d’, ‘e’]

So we first operate on partition(0, 4).
start = 0, end = 4
[‘a’, ‘b’, ‘c’, ‘d’, ‘e’]

We try to find the floor mid point index:
(0+4)/2 = 2, mid value is ‘c’

Now we have:

partition(0, 2) or partition([‘a’, ‘b’, ‘c’])
partition(3,4) or partition([‘d’, ‘e’])

Let’s work on the first one:

partition([‘a’, ‘b’, ‘c’])
floor mid point is (0+2)/2 = 1 [0, 1] mid value is ‘b’

Now we have:
partition(0, 1) or partition([‘a’, ‘b’])
partition(2,2) or partition([‘c’])

We try to find mid point index:
(0+1)/2 = floor (0.5) = 0

Now we have:

partition(0, 0) or partition([‘a’]) returns ‘a’
partition(1, 1) or partition([‘b’]). returns ‘b’

going up the recursion, partition([‘c’]) returns c.

Great.. so now we have values a, b, c. and finished [‘a’, ‘b’, ‘c’] at the top.

Now we need to process

partition([‘d’, ‘e’])

find mid point index (3+4)/2 = floor(3.5) = 3.

So we get

partition(3,3) returns ‘d’
and partition(4,4) returns ‘e’

2) The merging itself

The merging itself is quite easy.

  • Use a while loop, and compare the elements of both arrays IFF the cur for both arrays have not reached the end.
  • Whichever is smaller, goes into the result array.
  • Copy over leftover elements from the left array.
  • Copy over leftover elements from the right array.

Running Time

Running time for the double recursion

Average and Worst time:

O(n log n)

How?

The log n comes from the fact that merge sort is recursive in a binary way.

4 items, takes 2 divisions to get to the base items.
8 items, takes 3 divisions to get to the base items.

…if you keep going like this, you’ll see that its logarithmic in nature.

Running time for the merge

We are dividing the array along the recursive path.

So length n1 and n2 keeps changing and the complexity of merge routine/method at each call.

It is ‘n’ on the first call to recursion (leftArray of size n/2 and rightArray of size n/2)

It is ‘n/2’ on the second call to recursion. (we merge two n/4 arrays)

It is ‘n/4’ on the third call to recursion. (we merge two n/8 arrays)
……. and so on …..

till we merge just 2 items ( leftArray of size 1 and rightArray of size 1) and base case there is just one item, so no need to merge.

As you can see the first call to recursion is the only time the entire array is merged together at each level, a total of ‘n’ operations take place in the merge routine.

Hence that is why its O( n log n )

Azure: Create Node JS App and link it from GitHub to Azure Local Git

Database, Node JS

Assume you have a project on GitHub. We first use Azure, and create a LOCAL GIT. What this means is that we have a local git repository running on Azure. We then push our project from GitHub into the Azure local git.

make sure your code is simple.

Create Node JS Website, push it to GitHub, and clone it onto your Mac

https://github.com/Azure/azure-content/blob/master/articles/app-service-web/web-sites-nodejs-develop-deploy-mac.md

add_client_ip_firewall

Select Local GIT. This means that are going to push our project from GitHub, have a remote git here in Azure. Azure will provide us a git location via a GIT URL. We just put our files into that URL, and that’s it.

local-git

Make sure we create credentials for when we push our files from our local Mac, up into Azure’s local git.

deployment_credentials

Get the GIT URL
git_url

In our Mac’s local repository, we create a remote git location called ‘azure’. This means that we are to push our files/changes to that GIT location.

Make sure you are in your Mac’s local project directory (the where the .git folder is):

rickytsao$ git remote remove azure
rickytsao$ git remote add azure https://rtsao@myazurenodedemo.scm.azurewebsites.net:443/MyAzureNodeDemo.git
rickytsao$ git push azure master
Password for ‘https://rtsao@myazurenodedemo.scm.azurewebsites.net:443’:
Counting objects: 83, done.
Delta compression using up to 4 threads.
Compressing objects: 100% (79/79), done.
Writing objects: 100% (83/83), 13.19 MiB | 1.06 MiB/s, done.
Total 83 (delta 7), reused 0 (delta 0)
remote: Updating branch ‘master’.
remote: Updating submodules.
remote: Preparing deployment for commit id ‘fda61c8b1c’.
remote: Generating deployment script.

..you’ll also see it copying the files, then telling you the deployment is successful


remote: Copying file: ‘controllers\users\PUT_bbt~email.js’
remote: Copying file: ‘controllers\users\PUT_sign~email.js’
remote: Copying file: ‘controllers\users\PUT_~email.js’
remote: Copying file: ‘models\user.js’
remote: Looking for app.js/server.js under site root.
remote: Using start-up script server.js
remote: Generated web.config.
remote: The package.json file does not specify node.js engine version constraints.
remote: The node.js application will run with the default node.js version 4.2.3.
remote: Selected npm version 3.5.1
remote: …….
remote: npm WARN book_api@0.0.0 No repository field.
remote: Finished successfully.
remote: Running post deployment command(s)…
remote: Deployment successful.
To https://rtsao@myazurenodedemo.scm.azurewebsites.net:443/MyAzureNodeDemo.git
* [new branch] master -> master

Creating SQL Database

https://azure.microsoft.com/en-us/documentation/articles/sql-database-get-started/

Node Code

Further samples on SQL manipulation:
https://msdn.microsoft.com/library/mt715784.aspx

run “Node server.js” in a terminal

If you run your node app, you’ll see that your connection may have a problem because:

Basically, you have to go to your SQL server, and have the firewall allow access to your ip address like so:

sql_server_firewall

Stack based Memory Allocation

C/C++/Objective-C

https://en.wikipedia.org/wiki/Stack-based_memory_allocation

http://stackoverflow.com/questions/79923/what-and-where-are-the-stack-and-heap?rq=1

Stacks in computing architectures are regions of memory where data is added or removed in a last-in-first-out (LIFO) manner.

In most modern computer systems, each thread has a reserved region of memory referred to as its stack. When a function executes, it may add some of its state data to the top of the stack; when the function exits it is responsible for removing that data from the stack. At a minimum, a thread’s stack is used to store the location of function calls in order to allow return statements to return to the correct location, but programmers may further choose to explicitly use the stack. If a region of memory lies on the thread’s stack, that memory is said to have been allocated on the stack.

Because the data is added and removed in a last-in-first-out manner, stack-based memory allocation is very simple and typically faster than heap-based memory allocation (also known as dynamic memory allocation). Another feature is that memory on the stack is automatically, and very efficiently, reclaimed when the function exits, which can be convenient for the programmer if the data is no longer required. If however, the data needs to be kept in some form, then it must be copied from the stack before the function exits. Therefore, stack based allocation is suitable for temporary data or data which is no longer required after the creating function exits.