ref – https://www.khanacademy.org/computing/computer-science/algorithms/binary-search/a/implementing-binary-search-of-an-array

ref –

• https://www.digitalocean.com/community/tutorials/js-understanding-recursion
• https://medium.com/@reallygordon/implementing-memoization-in-javascript-5d140bb04166

prerequisites:

• http://chineseruleof8.com/code/index.php/2017/10/11/insertion-sort/
• https://www.khanacademy.org/computing/computer-science/algorithms/insertion-sort/a/analysis-of-insertion-sort

Given

Say we’re at the last element with the number 0:

[ 2, 3, 5, 7, 11, (0) ]

In order for 0 to be sorted, it must be compared to 11. Since 11 is larger is needs to slide over 1. This goes for all elements.
Thus, every element in the array has to slide over one position to the right. Then 0 gets inserted into arr[0]…ending up with [0, 2, 3, 5, 7, 11]

If we’re inserting element n into array with k elements, we use c to denote the # of lines of code to test an element (i.e 0) against an element and slide the element over.

For example, something like this:

then c in our case is 2 operations. But nevertheless, for implementation independent, c will simply denote the # of operations it takes to do the comparison and move the element over.

Thus, it took c * k to slide k elements over in place so that [X, 2, 3, 5, 7, 11] and finally we can insert 0 at the beginning [0, 2, 3, 5, 7, 11].

Worst case scenerio

Suppose that upon every call to insert, the value being inserted is less than every element in the subarray to its left.

Say we have [8, (5), 2, 1]

Insertion sort says, we always start index 1 (which is 5) and compare with previous element. We put 5 in a tmp variable and do a comparison, 5 < 8, so we slide over 8 over. This takes c steps and we do this 1 time. [8,8,2,1]

Then insert 5 at arr[0]

[5,8,2,1]

Then we move on to index 2, which is number 2.

[5,8,(2),1]

We do a comparison, 2 < 8, so we slide 8 over .. this is c. [5,8,8,1]

Then we compare 2 < 5, and we slide 8 over .. this is c. [5, 5, 8, 1]

Now we’re at index 0, so we simply fill it with our element 2.

[2,5,8,1]

So this is c * 2.

Then we move on to index 3, which is number 4.
We do the same comparison, and up with c * 3. Because we compare and move 1 step 3 times.

c * 1 + c * 2 + c * 3 executions.

Let’s say we start off with array [8, 7, 6 , 5, 4, 3, 2, 1]
We start at index 1 as stated by Insertion sort.

Then we work on 7. We compare and move (c) for k(1) element. So that’s c * 1. We get [7 8 6 5 4 3 2 1]
Then we work on 6. We compare and move twice for 8 and 7. So that’s c * 2. We get [6 7 8 5 4 3 2 1]
Then we work on 5. We compare and move for three times for 8 7 5. So that’s c * 3. We get [5 6 7 8 4 3 2 1]

And so on, up through the last time, when k = n-1 where n is the # of total elements.

Notice n-1. Why is that? Because we do not do compare element at index 1. We start at index 1.

Thus, what you get is:
c * 1 + c * 2 + c * 3 + c * 4 .. c * (n-1) = c(1+2+3+4…n-1)

That sum is an arithmetic series, except that it goes up to n-1, rather than n.

Arithmetic Series – Summation

Now let’s use Arithmetic series to simply and prove it.

To find the sum of the 1st n terms of an arithmetic sequence:

S = n (a initial + a of n) / 2

where n is # of terms
a initial = first term
a of n = last term

Given 5 10 15 20, let’s calculate the number of elements:

20 (last value) – 5 (first value) = 15
15 / 5 = 3
3 + 1 = 4. Add 1 to the total terms due to initial value 5.

The sum of these 4 terms are:

S = 4 (5 + 20)/2 = 2 (25) = 50
check it: 5 + 10 + 15 + 20 = 50 √

Given 2 4 6 8 10 12 14 16 18 20

S = 10 (2 + 20) / 2 = 5 (22) = 110
if you add it on the calculator, its 110 √

Say we want to go further say 2 to 222
222 – 2 = 220
220 / 2 = 110
110 + 1 = 111 Don’t forget to add 1 to 110 due to our initial value 2.
S = 111 (2 + 222)/2 = 12,432

We can also calculate term at n

A at n = initial a + (n-1)d

say we get 5 10 15 20 25

We want to figure out the 3rd term

2nd term = 5 + (2-1)(5) = 10 √
3rd term = 5 + (3-1)(5) = 15 √
5th term = 5 + (5-1)(5) = 25 √
…
…
100n term = 5 + (100-1)(5) = 500 √

The Proof

Using our formula for arithmetic series, we get that the total time spent inserting into sorted subarrays is

S = n (a initial + a of n) / 2

where # of terms n is n – 1 (remember, we don’t do the comparison for the place where we insert the value)
initial a is c * 1
last term a is c * (n – 1)

Thus, given:

c * 1 + c * 2 + c * 3 + c * 4 .. c * (n-1) =
c(1+2+3+4…n-1)

total # of terms = n-1
initial a = c*1
last term = c*(n-1)

Now we plug in everything:

S = (total # of terms) ( initial a + last term a ) / 2
S = (n-1)(c*1 + c*(n-1))/2
S = c * (n-1)(1 + n – 1) / 2
S = (c*n*(n-1)) / 2 = (cn^2)/2 – cn/2

Using O notation, we discard lower order cn/2, which leaves us (cn^2)/2
We also leave constants so we get rid of c and 1/2, which leaves us n ^ 2. Therefore, O(n^2)

Can we do it faster?

The answer is yes. Suppose we have the array [2, 3, 5, 7, 11], where the sorted subarray is the first four elements, and we’re inserting the value 11.

Upon the first comparison at index 1, we see that 3 > 2. So no need to shift. That’s c * 1.
Then we go to index 2. We see 5 > 2. So no need to shift. That’s c * 1.
This goes for 5, 7, and finally 11.

These are all constants time. Because there are n-1

This is c * (n-1), which is O(n)

So under the best case of already sorted elements, we can do O(n)

Running time of Random elements

Suppose that the array starts out in a random order. Then, on average, we’d expect that each element is less than half of the # of elements to its left. This means we expect c * (1 + 2 + 3 + … + n-1 ) / 2

The running time would be half of the worst-case running time. But in asymptotic notation, where constant coefficients don’t matter, the running time in the average case would still
be O(n^2).

Almost Sorted

What if you knew that the array was “almost sorted”: every element starts out at most some constant number of positions, say 17, from where it’s supposed to be when sorted? Then each call to insert slides at most 17 elements, and the time for one call of insert on a subarray of k elements would be at most c * 17.

Over all n-1 calls to insert, the running time would be at most 17 * c * (n-1).

which is O(n) just like the best case. So insertion sort is fast when given an almost-sorted array.

ref – https://www.geeksforgeeks.org/g-fact-86/#:~:text=Auxiliary%20Space%20is%20the%20extra,and%20space%20used%20by%20input.

Auxiliary Space is the extra space or temporary space used by an algorithm.

Space Complexity of an algorithm is the total space taken by the algorithm with respect to the input size. Space complexity includes both Auxiliary space and space used by input

Hence, Auxiliary Space is a subset of Space Complexity.

ref – https://tsh.io/blog/typescript-vs-javascript-comparison/

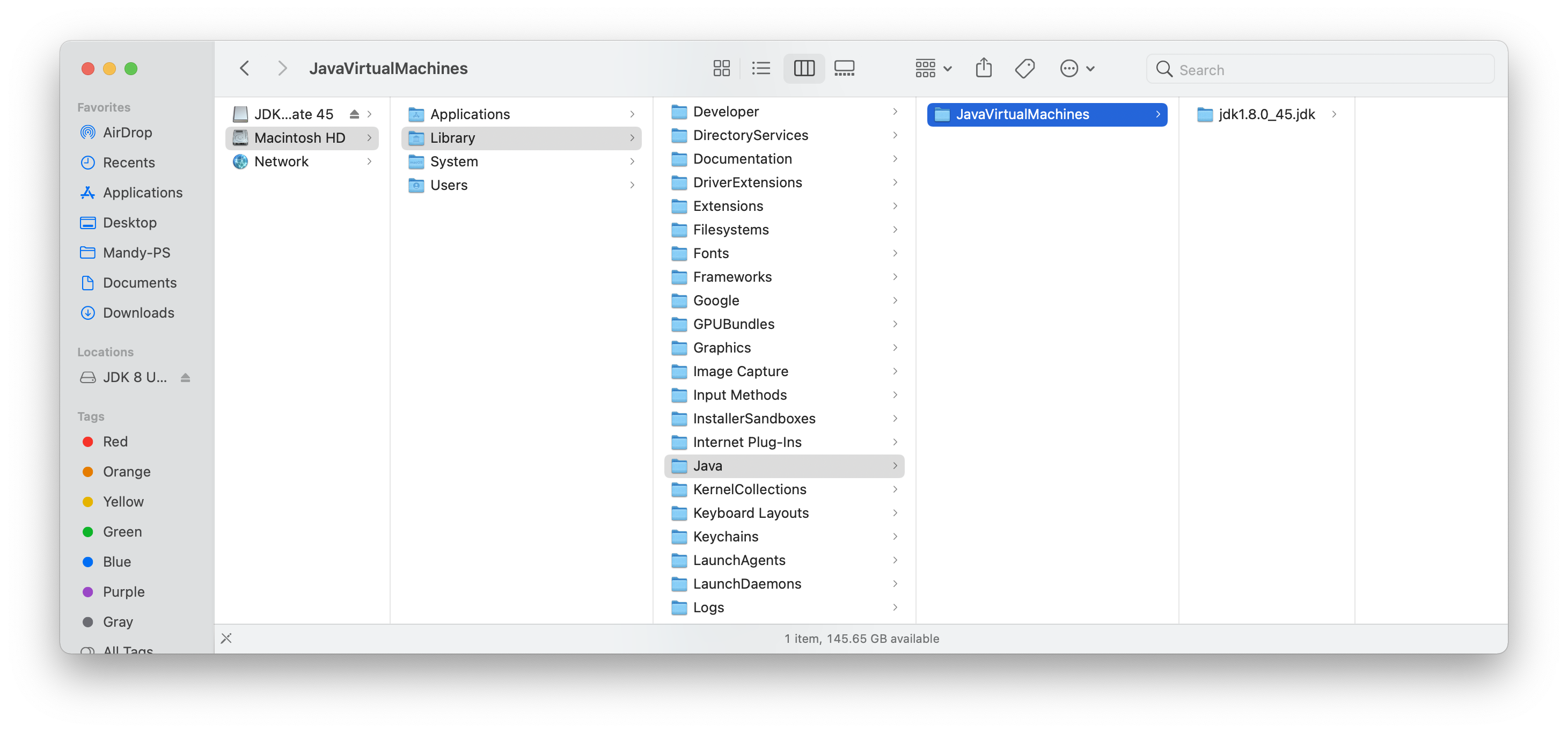
ref – https://www.delftstack.com/howto/java/change-java-version-mac/

To see what version of Java you have installed:

/usr/libexec/java_home -V

1.8.45.14 (x86_64) “Oracle Corporation” – “Java” /Library/Internet Plug-Ins/JavaAppletPlugin.plugin/Contents/Home
1.8.0_45 (x86_64) “Oracle Corporation” – “Java SE 8” /Library/Java/JavaVirtualMachines/jdk1.8.0_45.jdk/Contents/Home

In my case, when I decided to install an older version of JDK (jdk-8u45-macosx-x64), it installed at

java -version (note one dash)

java version “1.8.0_45”
Java(TM) SE Runtime Environment (build 1.8.0_45-b14)
Java HotSpot(TM) 64-Bit Server VM (build 25.45-b02, mixed mode)

So I’m using 1.8.0

Sometimes, it installs in other locations:

• https://blog.logrocket.com/run-react-native-apps-android-emulator-macos/
• https://javarepos.com/lib/jenv-jenv-java-general-utility-functions

brew install jenv

Updating Homebrew…
==> Downloading https://ghcr.io/v2/homebrew/portable-ruby/portable-ruby/blobs/sha256:0cb1cc7af109437fe0e020c9f3b7b95c3c709b140bde9f991ad2c1433496dd42
######################################################################### 100.0%
==> Pouring portable-ruby-2.6.8.yosemite.bottle.tar.gz
==> Auto-updated Homebrew!

After the command completes, we must tell our system where to look so it can use jenv, so we need to add it to our path. To do this, we must run the following command in our terminal:

echo ‘export PATH=”$HOME/.jenv/bin:$PATH”‘ >> ~/.zshrc
echo ‘eval “$(jenv init -)”‘ >> ~/.zshrc

We want to install JDK8 because that’s the version that works with our Android SDK Manager. Type the following into the terminal:

brew install adoptopenjdk8

brew install homebrew/cask-versions/adoptopenjdk8

This will install the latest version of Java 8 to a special directory in macOS. Let’s see which directory that is:

ls -1 /Library/Java/JavaVirtualMachines

adoptopenjdk-8.jdk

jenv add /Library/Java/JavaVirtualMachines/adoptopenjdk-8.jdk/Contents/Home/

openjdk64-1.8.0.292 added
1.8.0.292 added
1.8 added

jenv versions
system
1.8
1.8.0.292
15
15.0
* 15.0.2 (set by /Users/ricky_tsao/.java-version)
openjdk64-1.8.0.292
openjdk64-15.0.2

jenv info java
Jenv will exec : /Users/ricky_tsao/.jenv/versions/15.0.2/bin/java
Exported variables :
JAVA_HOME=/Users/ricky_tsao/.jenv/versions/15.0.2

java –version
openjdk 15.0.2 2021-01-19
OpenJDK Runtime Environment (build 15.0.2+7-27)
OpenJDK 64-Bit Server VM (build 15.0.2+7-27, mixed mode, sharing)

jenv doctor
[OK] No JAVA_HOME set
[OK] Java binaries in path are jenv shims
[OK] Jenv is correctly loaded

ref – http://chineseruleof8.com/code/index.php/2019/01/03/functions-are-first-class-objects-js/

function vs procedure

Procedure – collection of functionalities.
May or may not have input, or return values, and have multiple tasks.

Functions – Mathematical functions.

• Have input
• Return value
• Simplified to a single task
• Easy for reuse

Step 1

We first have a string literal.
We have a function called prepareString.

And by scope, it reference the str and trims it for str1.
Then str1 replaces it with regex for str2.
Finally str2 upper cases everything for str3.
str3 then splits into an array.

Finally we loop through this array and try to find A, AN, or THE. If its found, delete it using splice.

Step 2 – separate them into one task functions

becomes

becomes

becomes

becomes

becomes

Using noArticles:

becomes

Step 3

Then we need to change these functions into arrow functions.

Step 4 – Optionally call them together

pipe

The pipe function goes through each function and applies the accumulator string to each function..starting with the initiator x.

So if x is ‘word’, and the first function is !${param}, this will return ‘!word’.
Then the 2nd function is *${param}, then we’d get ‘*!word’.

Basically, it would apply the result of the current function to the param of the next function.

Notice our spread operators in the parameter. Its taking all the params together and bringing them together as the array fns.

Our output would be:

$word
!$word
(!$word)
*(!$word)
*(!$word)–>
<--*(!$word)-->

We can also start from the right function, (by using reduceRight) so now our output would like this:

<--word <--word-->
*<--word-->
(*<--word-->)
!(*<--word-->)
$!(*<--word-->)

Now, going back to our work, we would stick each function to process on the string. Then use the returned string as the input for the next function. Literally, the functions put together act as a pipe for strings to go through and be processed.

Function Composition 2

Given…

and situation is:

1) Convert each statement to a function that can accept and act on any array.

2) Compose a function that will remove both zero or lower scores and scores over 100. Test it using the scores array.

3) Compose a function that will do all the modifications to an array. Test it using the scores array.

4) Create a function that will accept an array and return the average. Use the function that sums scores and the function that counts scores or the length property.

5) Compose a function that will do all the modifications on an array and return an average.

Arity

So we still have our pipe function. Remember that it takes in an array of functions, and an initial string x. (Henry)

It goes through the first function and gives ‘Henry’ as the first parameter. The return value of the 1st function (user object) is then inserted into the 2nd function.

The return value of the 2nd function is then inserted into the 3rd function, so on and so forth.

users array is the data that will be bind to getUsers function.

As you can see we a function like so:

We need to change it using bind so that we can pass in users as the data, and we get a reference to it all. That way, users is matched up to param arr.

We get partGetUser, and then when we execute it inside pipe, we can pass in ‘Henry’ to param name of getUser.

storeUser is just a standard function.

we have our cloneObj that takes an object and clones it using JSON. We leave it as is.

Then we have updateScore:

we need to change it like this:

updateTries is used as is.

We put updateUser, cloneObj, partUpdateScore30, and updateTries into our pipe utility function.
We get the result back when ‘Henry’ is inserted into the beginning of the pipe.

Arity full code

Building software by creating pure functions, avoid shared state, mutable data, and side-effects.

application state flows through pure functions.

Side Effects and Pure Functions

Notice the data is the array of users.
We have our mutable function that literally uses scope to access users and change its contents.

For the pure functions we take in parameters, and we do not modify these inputs. Instead, we return new arrays with shallow copied data. Notice we never touch param arr, nor name. We simply get the data we need, and return new arrays.

We then use the pure functions to calculate new scores.
Then give it to our mutable functions to update our data.

Avoid Shared State

Javascript stores data in objects and variables. This is called state.

Notice how users are shared via closure scope. We need to void this by passing state (users)
from one function to another.

Mutation

how to avoid mutating? Clone it

but…for objects with nested data:

we need to convert it to string, then parse it back into an object.

We can do the same with arrays:

Object.assign and spread operator works the same way.

For Arrays, spreading a null would give an error

For Objects, both silently exclude the null value with no error.