ref – https://en.wikipedia.org/wiki/Associative_array
https://github.com/redmacdev1988/LinkedListHashTable
Open hashing – in this strategy, none of the objects are actually stored in the hash table’s array; instead once an object is hashed, it is stored in a list which is separate from the hash table’s internal array. “open” refers to the freedom we get by leaving the hash table, and using a separate list. By the way, “separate list” hints at why open hashing is also known as “separate chaining”.
The most frequently used general purpose implementation of an associative array is with a hash table: an array combined with a hash function that separates each key into a separate “bucket” of the array. The basic idea behind a hash table is that accessing an element of an array via its index is a simple, constant-time operation. Therefore, the average overhead of an operation for a hash table is only the computation of the key’s hash, combined with accessing the corresponding bucket within the array. As such, hash tables usually perform in O(1) time, and outperform alternatives in most situations.
Hash tables need to be able to handle collisions: when the hash function maps two different keys to the same bucket of the array. The two most widespread approaches to this problem are separate chaining and open addressing.
https://en.wikipedia.org/wiki/Hash_table#Separate_chaining
Average | Worst Case
Space O(n)[1] | O(n)
Search O(1) | O(n)
Insert O(1) | O(n)
Delete O(1) | O(n)
The idea of hashing is to distribute the entries (key/value pairs) across an array of buckets. Given a key, the algorithm computes an index that suggests where the entry can be found:
index = f(key, array_size)
hash = hashfunc(key) // where hash is some number
index = hash % array_size // in order to fit the hash into the array size, it is reduced to an index using modulo operator
In this method, the hash is independent of the array size, and it is then reduced to an index (a number between 0 and array_size − 1) using the modulo operator (%) .
Choosing a hash function
http://eternallyconfuzzled.com/tuts/datastructures/jsw_tut_hashtable.aspx
Table size and range finding
The hash functions introduced in The Art of Hashing were designed to return a value in the full unsigned range of an integer. For a 32-bit integer, this means that the hash functions will return a value in the range [0..4,294,967,296). Because it is extremely likely that your table will be smaller than this, it is possible that the hash value may exceed the boundaries of the array.
The solution to this problem is to force the range down so that it fits the table size.
For example, if the table size is 888, and we get 8,403,958, how do we fit this value within the table?
A table size should not be chosen randomly because most of the collision resolution methods require that certain conditions be met for the table size or they will not work correctly. Most of the time, this required size is either a power of two, or a prime number.
Why a power of two? Because we use bitwise operation to get performance benefits. Bitwise operations are done on binary bit combinations and thus, that’s why the table size needs to be in power of 2. A table size of a power of two may be desirable on some implementations where bitwise operations offer performance benefits. The way to force a value into the range of a power of two can be performed quickly with a masking operation.
For example, to force the range of any value into eight bits, you simply use the bitwise AND operation on a mask of 0xff (hexadecimal for 255):
0x8a AND 0xff = 0x8a
from hex to digit:
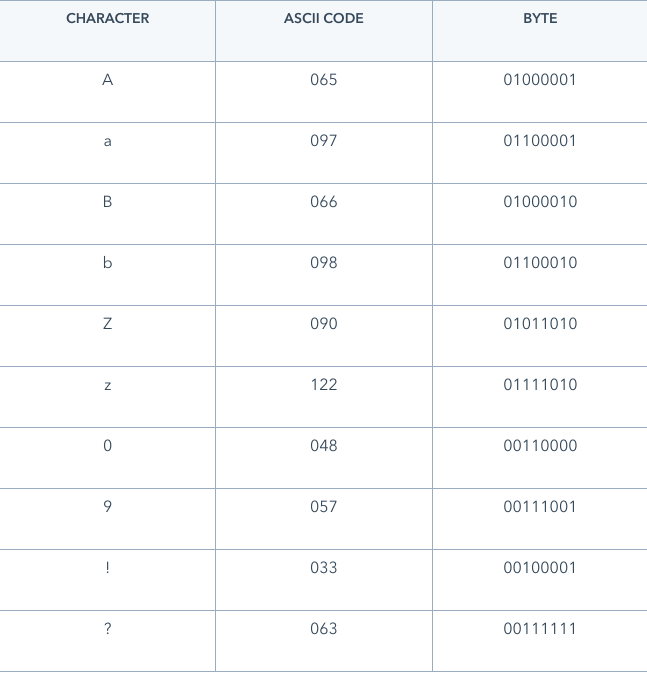
Note that _ _ _ _ _ _ _ _ = 8 bits = 1 byte.
2 2 2 2 2 2 2 2 = 2^8 = 256 representations (memory addresses)
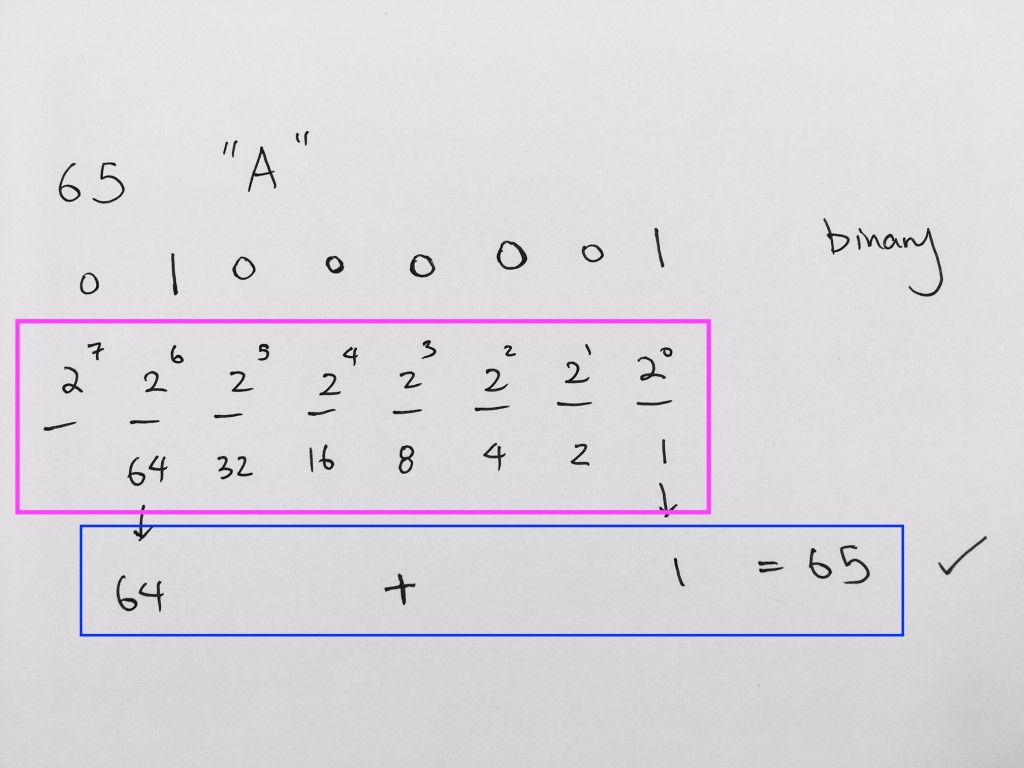
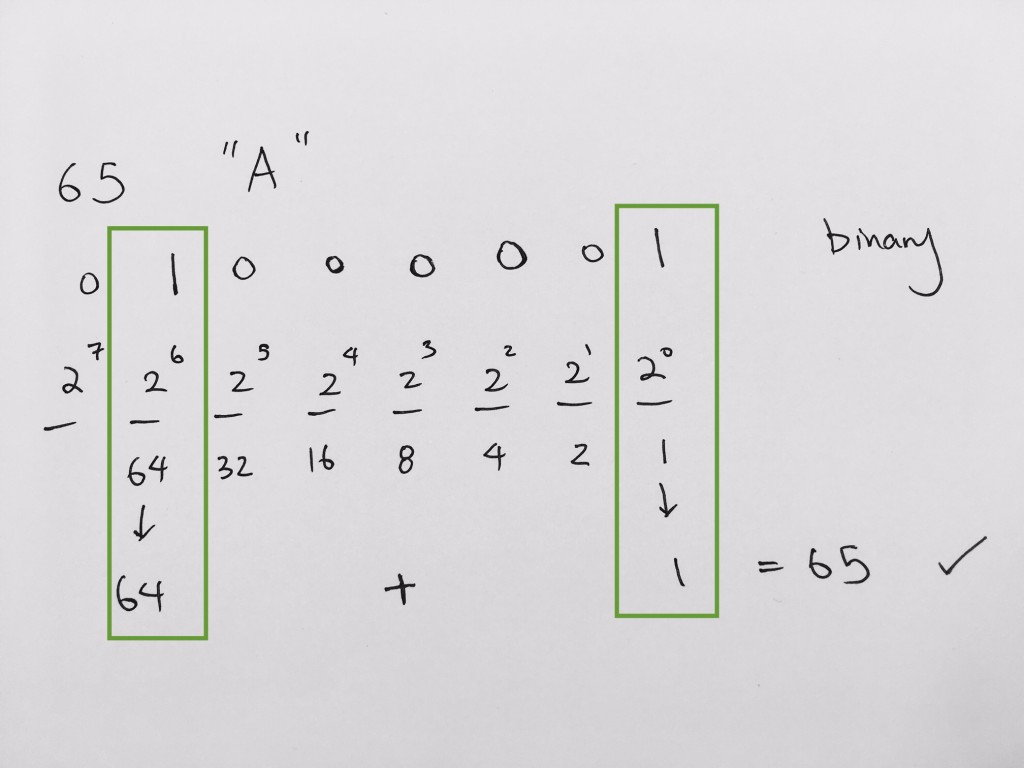
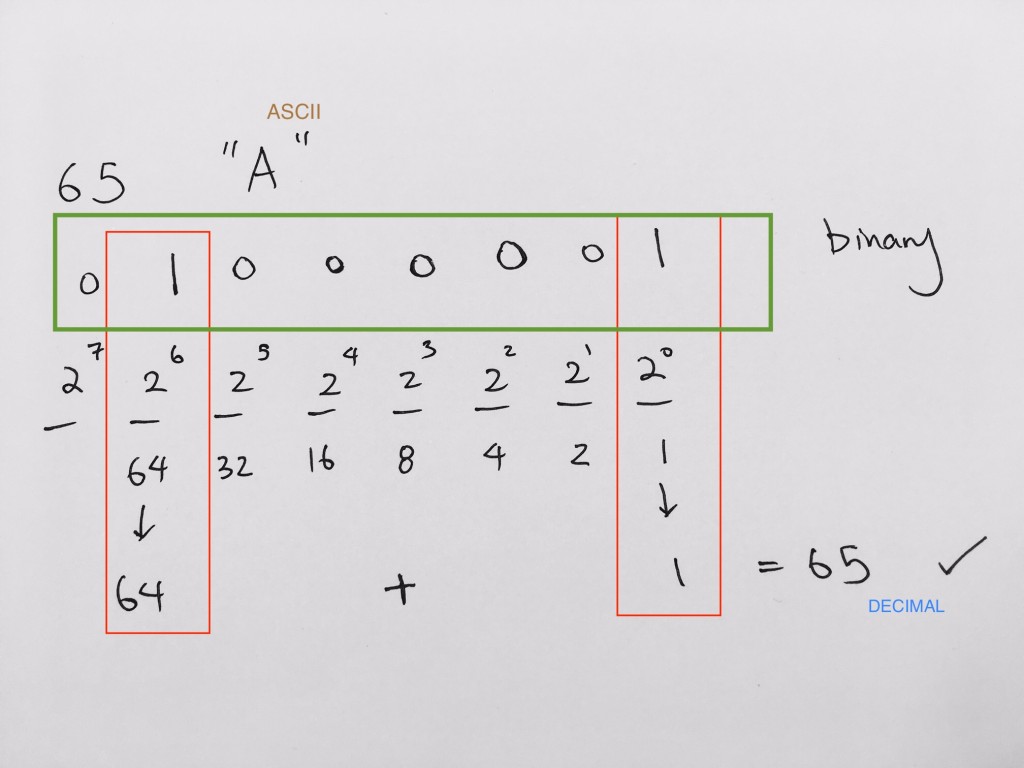
0x8a -> 1000(8) 1010(a) -> 1000 1010 binary
binary to decimal is 1 * 128 + 0 * 64 + 0 * 32 + 0 * 16 + 1 * 8 + 0 * 4 + 1 * 2 + 0 * 1 = 128 + 10 = 138.
from digit to hex:
Thus, if we were to get a value of 138, we force this value to give us a return index from an array size of 8 bits by using AND operation with 0xff.
Thus, in code, you’ll get the parameter 138. Then you convert it to 1000 1010, then to hex which is 0x8a.
Then you apply the AND bit op which gives you 0x8a AND 0Xff = 0x8a
so 138 in 256. But what if you get some large number like 888?
888 in binary is 0x378
0x378 AND 0x0ff = 78
we append 0 to front of 0xff because we’re dealing with 3 hex places. We apply the AND and get 78. Thus if you get hash value 888, it would give you index 78.
table[hash(key) & 0xff]
This is a fast operation, but it only works with powers of two. If the table size is not a power of two, the remainder of division can be used to force the value into a desired range with the remainder operator. Note that this is slightly different than masking because while the mask was the upper value that you will allow, the divisor must be one larger than the upper value to include it in the range. This operation is also slower in theory than masking (in practice, most compilers will optimize both into the same machine code):
table[hash(key) % 256]
When it comes to hash tables, the most recommended table size is any prime number.
This recommendation is made because hashing in general is misunderstood, and poor hash functions require an extra mixing step of division by a prime to resemble a uniform distribution. (https://cs.stackexchange.com/questions/11029/why-is-it-best-to-use-a-prime-number-as-a-mod-in-a-hashing-function)
Another reason that a prime table size is recommended is because several of the collision resolution methods require it to work. In reality, this is a generalization and is actually false (a power of two with odd step sizes will typically work just as well for most collision resolution strategies), but not many people consider the alternatives and in the world of hash tables, prime rules.
Advantages in using Hash Table
The main advantage of hash tables over other table data structures is speed. This advantage is more apparent when the number of entries is large. Hash tables are particularly efficient when the maximum number of entries can be predicted in advance, so that the bucket array can be allocated once with the optimum size and never resized.
If the set of key-value pairs is fixed and known ahead of time (so insertions and deletions are not allowed), one may reduce the average lookup cost by:
1) a careful choice of the hash function,
2) bucket table size,
3) internal data structures.
In particular, one may be able to devise a hash function that is collision-free, or even perfect. In this case the keys need not be stored in the table.
Open Addressing
Another popular technique is open addressing:
- at each index of our list we store one and one only key-value pair
-
when trying to store a pair at index x, if there’s already a key-value pair, try to store our new pair at x + 1
if x + 1 is taken, try x + 2 and so on… - When retrieving an element, hash the key and see if the element at that position (x) matches our key. If not, try to access the element at position x + 1. Rinse and repeat until you get to the end of the list, or when you find an empty index — that means our element is not in the hash table
Separate chaining with linked lists
Chained hash tables with linked lists are popular because they require only basic data structures with simple algorithms, and can use simple hash functions that are unsuitable for other methods.
The cost of a table operation is that of scanning the entries of the selected bucket for the desired key. If the distribution of keys is sufficiently uniform, the average cost of a lookup depends only on the average number of keys per bucket—that is, it is roughly proportional to the load factor.
For this reason, chained hash tables remain effective even when the number of table entries n is much higher than the number of slots. For example, a chained hash table with 1000 slots and 10,000 stored keys (load factor 10) is five to ten times slower than a 10,000-slot table (load factor 1); but still 1000 times faster than a plain sequential list.
For separate-chaining, the worst-case scenario is when all entries are inserted into the same bucket, in which case the hash table is ineffective and the cost is that of searching the bucket data structure. If the latter is a linear list, the lookup procedure may have to scan all its entries, so the worst-case cost is proportional to the number n of entries in the table.
The bucket chains are often searched sequentially using the order the entries were added to the bucket. If the load factor is large and some keys are more likely to come up than others, then rearranging the chain with a move-to-front heuristic may be effective. More sophisticated data structures, such as balanced search trees, are worth considering only if the load factor is large (about 10 or more), or if the hash distribution is likely to be very non-uniform, or if one must guarantee good performance even in a worst-case scenario. However, using a larger table and/or a better hash function may be even more effective in those cases.