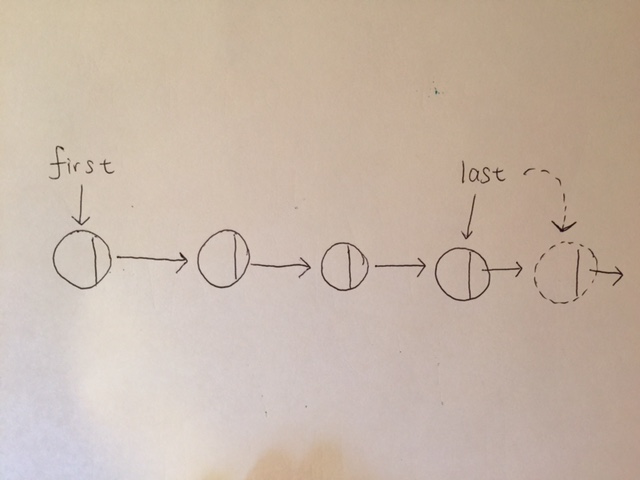download source

Queue is First In First Out, FIFO.
This means that Nodes are processed in order. They get in line, and each node is taken care of in the order added (or received).

In order to do this, we have a first and a last pointer. The first pointer points to the beginning of the list, which represents the next node to be processed and removed first.

The last pointer points to the end of the list, which represents the newest node that comes in, and thus, must wait its turn for the list to process and remove it.

The first pointer points to the node TO BE processed and thus removed.

The last pointer points to the position where new, incoming nodes come in.

source download

Stacked list is all about having ONE head pointer.

Pop is O(1)
Push is O(1)

The head pointer is used to add and remove.

For append:

1) We have head point to NULL in the beginning

2) First item is initialized through being supplied with values from its constructor parameters. These parameters are int data, and whatever head is pointing to.

If we’re starting out, head should be pointing to NULL. If there were previous items, then head should be pointing to the latest pushed item.

3) In the case of appending the first node, our first node’s pNext should be to what head is pointing to, which is NULL.

4) our head then re-points to the newly created Node object. Our first object as been appended.

For pop, its about having a temp pointer pointing to the head, then have the head traverse 1 step forward. Then delete the object that temp is pointing to.

source code

• A simple linked list in C++
• Basic features
• Running time

Features

– add by appending
– search
– remove
– display

A linked list is a bunch of nodes ‘linked’ together by pointers. Each node has a ‘next’ pointer that points tot he next node. This is what creates the link.

First step is to create the node. The node has data and a next pointer. The next pointer should be of the same type this node because after all, the nodes are of the same type.

You’d want to have 2 constructors for the Node. An default empty one, and another where you can assign new values.

Node.h

Node.cpp

LinkedList.hpp

Append

1) We have head point to NULL in the beginning

2) First item is initialized through being supplied with values from its constructor parameters. These parameters are int data, double priority, and whatever head is pointing to.

3) In the case of appending the first node, our first node’s pNext should be to what head is pointing to, which is NULL

4) our head then re-points to the newly created Node object. Our first object as been appended.

In programming, we always execute the inner most first. Then we work our way out.

The inner most is the data parameters.

First, we evaluate data to be a int. We evaluate priority to be a double. Finally, we evaluate head to point to NULL.

Then we pass these 3 values into the constructor of Node. Node object gets created with its attributes initialized. The values are initialized to , and the pNext pointer points to what head is.

Finally, when the Node object has been created, we have our head point to this Node object.

Remove

temp means the temporary node we’re on. Trailer means the pointer behind temp, so that when we remove, we can use the trailer to connect the link.

The important to notice here is

1) evaluating the first item. When temp and trailer are pointing to the same node, we’re at the first node. When we see a match, we remove the node and repoint head to the next node.

2) Moving forward to evaluate the next item involves simply checking to see if we have a match or not. If there NO match we move forward by first, pointing trailer to temp. Then have temp point to temp->next. That way, when temp has a match, then the trailer can link (the node before and after the deleted node) together.

Running Time

Search O(n)
Delete O(n)
Append O(1)

Finding or deleting a specified item requires searching through, on the average, half the items in the list. This requires O(N) comparisons.

An array is also O(N) for these operations, but the linked list is nevertheless faster because nothing needs to be shifted when an item is inserted or removed.

The increased efficiency can be significant, especially if a copy takes much longer than a comparison.

Of course, another important advantage of linked lists over arrays is that the linked list uses exactly as much memory as it needs, and can expand to fill all available memory. The size of an array is fixed when it’s created; this usually leads to inefficiency because the array is too large, or to running out of room because the array is too small.

Vectors, which are expandable arrays, might solve this problem to some extent, but they usually expand in fixed-sized increments (such as doubling the size of the array whenever it’s about to overflow). This use of memory is still not as efficient as a linked list.

In an array, any item can be accessed, either immediately through its index, or by searching through the sequence of cells until its found.

In stacks and queues, however, access is restricted. Only one item can be read or removed at a given time.

Their interface is designed to enforce this restricted access. Theoretically, access to other items are not allowed.

Stacks and Queues are abstract by nature. What I mean by that is that they are defined by their interface. Their underlying workings can be different. For example, A stack may have push, pop, view, etc as its interface. But the underlying mechanism may be an array of a linked list.

Some ways to use Stacks

Reverse a word

Use a stack to reverse a word. When a string of word comes in, push each character into your stack. Then pop the stack onto an empty string, and you will then have the word reversed.

Delimiter Matching

Another common use for stacks is to parse certain kinds of text strings. The delimiters are (, ), [, ], {, }…etc.

You have an empty stack

You have a string say “a{b(c[d]e)f}”

read “a”
“a” != delimiter, go on.
Stack:

read “{”
“{” is opening delimiter, push onto stack.
Stack: {

read “b”
“b” != delimiter, go on.
Stack: {

read “(”
“(” is opening delimiter, push onto stack.
Stack: { (

read “c”
“c” != delimiter, go on.
Stack: { (

read “[”
“[” is opening delimiter, push onto stack.
Stack: { ( [

read “d”
“d” != delimiter, go on.
Stack: { ( [

read “]”
“[” is closing delimiter, pop from stack.
Stack: { (

read “e”
“e” != delimiter, go on.
Stack: { (

read “)”
“)” is closing delimiter, pop from stack.
Stack: {

read “f”
“f” != delimiter, go on.
Stack: {

read “}”
“}” is closing delimiter, pop from stack.
Stack:

Using Queues

Queues are first in first out.

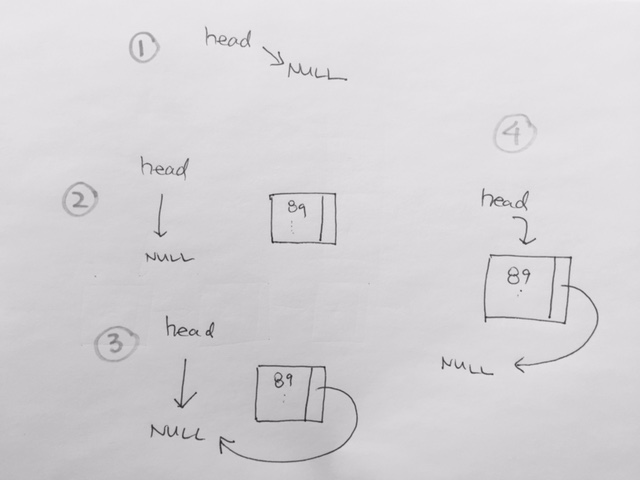
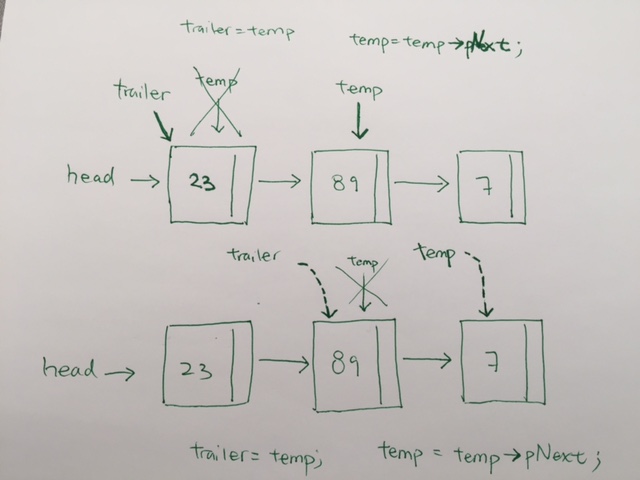
In Arrays, when we insert, we just push onto the array, which is O(1).
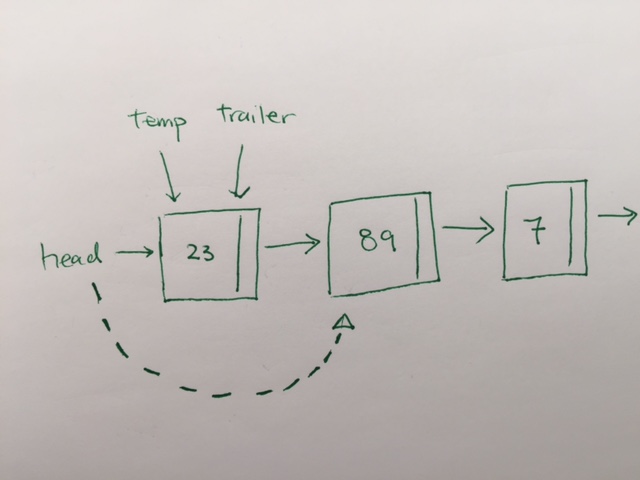
When we delete, we remove the 0th element, then push all the elements down, which is O(n).

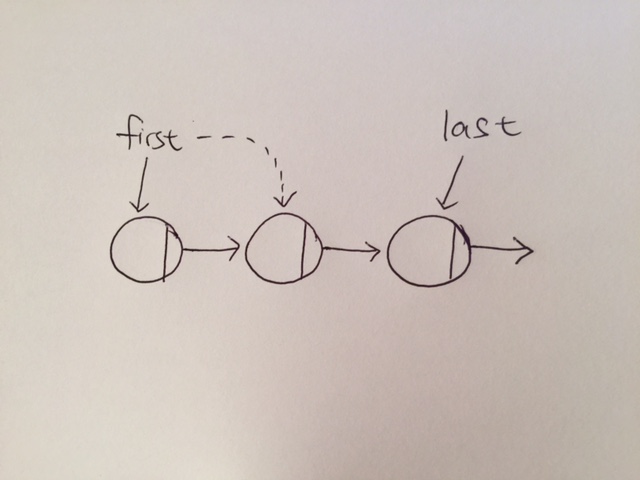
In linked list, we have head and tail pointer. This would make both adding and removing O(1).

However, search and delete would be O(n) because on average, it takes n/2 where n is number of items. T = k * (n/2) where constants are included T = n. In regards to how fast it is to the number of items, we have T = O(n)

priority queues

0 is highest priority, a larger number means a lower priority.

Thus, when we insert an item, we start at the very end of the array. Use a for loop back to 0th index, and see if the new element is larger than the element at the index.

The new element being a larger element means it has a lower priority. If it is, we shift the array element up. We keep doing this until our priority is properly inserted. Having the smallest number mean we have a higher priority, thus, we append the element at the top.

When we delete, we simply pop the top element.

http://www.codenlearn.com/2011/07/understanding-algorithm-complexity.html
https://www.quora.com/How-would-you-explain-O-log-n-in-algorithms-to-1st-year-undergrad-student

Hardware execution time

Let’s say an assignment

is one step.

This requires the same amount of time no matter how big the length of array is. We can say that time, T, to insert an item into an unsorted array is a constant K:

T = K

In detail, the actual time (in ms or whatever unit of measure) is required by the insertion is:

• related to the speed of the microprocessor
• how efficiently the compiler has generated the program code
• ..other factors

Linear Search

The number of comparisons that must be made to find a specified item is, ON AVERAGE, half of the total number of items. Hence, if N is the total number of items, the search time T is

N = number of items
T = time
K = execution time of hardware

T = K * (N / 2)

For a handier formula, we can lump the 1/2 into the K, because we are dealing with constant numbers. Hence we can say a constant K is
some constant K which represents execution time of the hardware divided by 2.

Hence, T = K * N

Time = hardware execution time * Number of items

The reason why we do this is because, we’re not interested in the actual execution time. We’re just interested in how fast the algorithm is running IN ACCORDANCE TO THE NUMBER OF ELEMENTS N.

Thus, whatever execution time is for the particular processor and compiler at the time does not matter to us. Whether its a 333mhz processor or a 3ghz processor, it doesn’t matter.

We just lump that constant numeric together and pull out the number of elements N SO THAT we can convey how running times are affected by the number of items.

This says that average linear search times are proportional so the size of the array.

For example,

In an unordered array, Search takes O(N) time because you need to go through N/2 elements on average. Multiple that that by processing time constant K time T = (N/2) * K = K * N = O(N) where we don’t care about literal processing time of K.

In an unordered array, Deletion takes O(N) time because once you use Search to find the element to delete, you still need to shift elements down to fill the empty spot. On average its N/2 elements that you need to shift down. Multiple that by processing time constant K time T = (N/2) * K = K * N = O(N) where we don’t care about processing time of K.

Binary Searching

T is time
K is hardware execution time
N is number of items

T = K * log (base 2) N

But because whether we’re dealing with binary three, or tinery tree, or whatever, base 2, base 3…etc is simply a constant numeric. i.e lay out a base 2 framework and a base 10 framework, their difference is 3.322. That’s a numeric that we can include into the constant K.

Hence, T = K * log N.

Eliminating the Constant K for Big O

When comparing algorithms you don’t really care about the particular microprocessor chip or compiler, all you want to compare is how T changes for different values of N. Therefore, the constant isn’t needed.

Big O notation uses the uppercase letter O, which you can think of as meaning “order of”. In Big O notation, we would say that a linear search takes O(N) time, binary search takes O(log N) time. Insertion into an unordered array takes O(1), or constant time.

The idea in Big O notation isn’t to give an actual figure for running time, but to convey how running times are affected by the number of items.

Log(n)

In the case of binary search, you are trying to find the maximum number of iterations, and therefore the maximum number of times the search space can be split in half.

This is accomplished by dividing the size of the search space n, by 2 repeatedly until you get to 1 number.

Let’s give the number of times you need to divide n by 2 the label x. Since dividing by 2 x times is equivalent to dividing by 2^x, you end up having to solve for this equation:

n total number of items
x number of times you need to divide by 2 to get the result 1

n / 2^x = 1

x is the number of times you can split a space of size n in half before it is narrowed down to size 1.
The solution to this equation be found by taking the logarithm of both sides:

2^x = n

by log mathematical inductions….

log (2^x) = log (n^1)

x log 2 = 1 * log n

x = log ( n ) / log ( 2 ) = log base 2 (n)

Hence

x = log base 2 (n)

means that given n numbers, x is the number of times we split those n numbers in half, in order to get a result of 1.