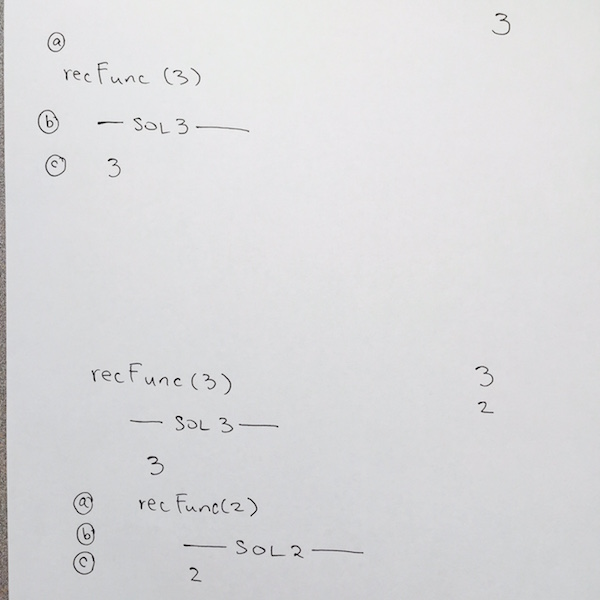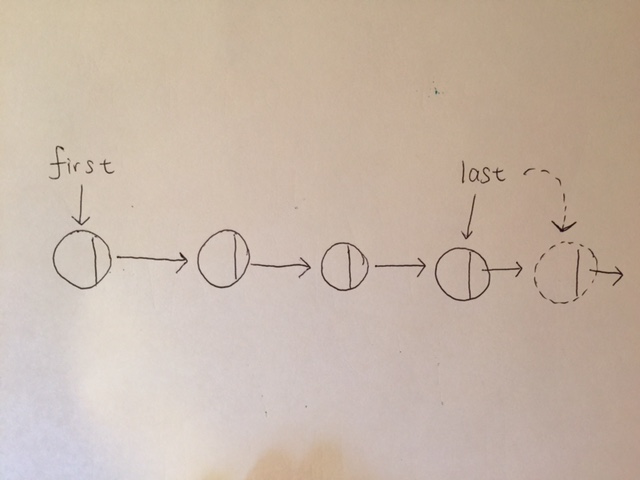All posts by admin

Binary Array Search

November 27, 2015algorithmsadmin

#include <stdio.h>

#include <ctime>

#include <cstdlib>

class OrdArray

{

private:

int * integerArray;

int nElems;

public:

OrdArray(int max) //constructor

{

nElems = max;

integerArray = new int [max];

//srand((unsigned)time(0)); // initialize the RNG

for ( int i = 0; i < getSize(); i++)

{

integerArray[i] = i + 2;

}

//parameter is the element that we want to find

int find(int elementToFind) //initial find()

{

printf("\n\nI want to find element: %d in the array", elementToFind);

return recFind(elementToFind, 0, nElems-1);

}

int recFind(int elementToFind, int lowerBound, int upperBound)

{

if(upperBound < lowerBound) {

printf("\n\n ------- DOES NOT EXIST------");

return -1;

}

printf("\n\n Let's check if element %d is at 'floor middle' of index %d to index %d?", elementToFind, lowerBound, upperBound);

int floorMiddleIndex = (lowerBound + upperBound ) / 2;

printf("\nThe element at middle floor index %d is: %d",

floorMiddleIndex, integerArray[floorMiddleIndex]);

int floorMiddleElement = integerArray[floorMiddleIndex];

if(floorMiddleElement == elementToFind) {

printf("\n\nYES! FOUND IT!");

return floorMiddleIndex; //found it

}

else {

//if we're looking for is larger than our floor middle element,

//then we go to upper half of array

if (floorMiddleElement < elementToFind) {

printf("\ngoing to search from index %d to index %d", floorMiddleIndex+1, upperBound);

return recFind(elementToFind, floorMiddleIndex+1, upperBound);

}

else { //floorMiddleElement >= elementToFind

printf("\ngoing to search from index %d to index %d", lowerBound, floorMiddleElement-1);

return recFind(elementToFind, lowerBound, floorMiddleIndex-1);

}

return -1;

}

int getSize() {

return nElems;

}

void display() {

printf("\n\n");

for (int i = 0; i < nElems; i++) {

printf("\n array element %d: %d", i, *(integerArray+i));

}

};

Pre print recursion

November 16, 2015algorithmsadmin

ref – http://chineseruleof8.com/code/index.php/2015/11/16/simple-recursion/

void countDown( int n ) {

//SOL #1

if(n == 0){ // BASE CASE #2

printf("\n\n ~~~ HAPPY NEW YEARRRRRR! ~~~~ "); //#3

return; //EOL #4

}

printf("\n\n %d !", n); // #5

countDown(n-1); //#6

//EOL #7

}

note: recFunc is a placeholder name for any recursive function name that you are running.

a) we write the push of the function for recFunc( 3 ) onto the main stack
b) We begin for the start of line for recFunc( 3 ) at comment #1
c) We check the base case at comment #2, it is false so we move down to comment #5. Its a print statement so we print n, which is 3.

We need to remember to write 3 in the output as shown on the top right hand side of the image.

Then we hit comment #6, which is a call to the recursive function. This means we are going to push recRunc( 2 ) onto the stack. Thus:

a) we for visual clarity, we tab some spaces, then write out recFunc( 2 )
b) we reach comment #1 which is the Start Of Line for recFunc( 2 )
c) We check the base case at comment #2, it is false so we move down to comment #5. Its a print statement so we print n, which is 2. Remember to write it in your output section.

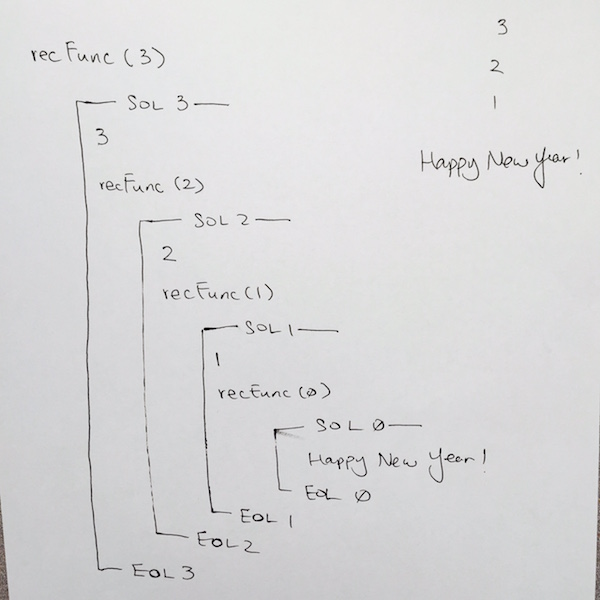
Reaching the base case

We continue this fashion until we hit recFunc( 0 ). Once we get to recFunc( 0 ), we write out SOL at comment #1, then when we reach the base case at comment #2. It evaluates to true, so we print out the “happy new year” at comment #3, and the function returns at comment #4.

Whenever a return or end of function is reached, we pop the stack frame. In our case we pop the stack frame for recFunc( 0 ). On our paper for visual clarity, make sure you draw a line connecting SOL 0 to EOL 0. This tells us that the stack frame for rechFunc has been popped and completed.

In code, we then continue where we left off at comment #6 for recFunc( 1 ). We then go down to comment #7. Its the EOL for recFunc( 1 ), so on our paper, we write out —– EOL 1 —–.

In code, we reach end of function, so that means we pop the stack frame for recFunc( 1 ). Make sure you draw the connecting line from SOL 1 TO EOL 1 to clarify this.

We continue where we left off at comment #6 for recFunc( 2 )…

We keep doing this until all the stack frames have been popped, and we finish running recFunc( 3 ).

Thus, in the output, you should see: 3 2 1 Happy New Year!

Recursion Concepts

November 16, 2015algorithmsadmin

ref – https://www.cs.drexel.edu/~mcs172/Su04/lectures/07.3_recursion_intro/Dangers.html?CurrentSlide=7
https://en.wikipedia.org/wiki/Recursion_termination

Recursion in computer science is a method where the solution to a problem depends on solutions to smaller instances of the same problem. In other words, when a function calls itself from its body.

The power of recursion lies in the possibility of defining an infinite set of objects by a finite statement. In the same manner, an infinite number of computations can be described by a finite recursive program, even if this program contains no explicit repetitions.

A common computer programming tactic is to divide a problem into sub-problems of the same type as the original, solve those sub-problems, and combine the results. This is often referred to as the divide-and-conquer method;

Pros

Less Code – Recursion is generally known as Smart way to Code
Time efficient – If you use recursion with memorization, Its really time saving

For certain problems (such as tree traversal ones) – it’s more intuitive and natural to think of the solution recursively.

Cons

Recursion takes up large amounts of computer resources storing return addresses and states.
In other words, if left unbounded, and fed a data set which leads it deep enough, the function call overhead will accumulate, sucking up system resources rapidly and eventually overflowing the stack.

It is fairly slower than its iterative solution. For each step we make a recursive call to a function, it occupies significant amount of stack memory with each step.

May cause stack-overflow if the recursion goes too deep to solve the problem.
Difficult to debug and trace the values with each step of recursion.

Recursion vs Iteration

Now let’s think about when it is a good idea to use recursion and why. In many cases there will be a choice: many methods can be written either with or without using recursion.

Q: Is the recursive version usually faster?
A: No — it’s usually slower (due to the overhead of maintaining the stack)

Q: Does the recursive version usually use less memory?
A: No — it usually uses more memory (for the stack).

Q: Then why use recursion??
A: Sometimes it is much simpler to write the recursive version (for trees)

Use recursion for clarity, and (sometimes) for a reduction in the time needed to write and debug code, not for space savings or speed of execution.
Remember that every recursive method must have a base case (rule #1).
Also remember that every recursive method must make progress towards its base case (rule #2).
Sometimes a recursive method has more to do following a recursive call. It gets done only after the recursive call (and all calls it makes) finishes.
Recursion is often simple and elegant, can be efficient, and tends to be underutilized.

Examples

void countDown( int n ) { //n is the counter

//SOL Start Of Line #1

//base #2

if(n == 0) {

printf("\n\n ~~~ HAPPY NEW YEAR! ~~~~ "); // #3

//EOL #4

return;

}

countDown(n-1); //recursion #5

//EOL End Of Line #6

}

Every recursive function has 2 basic parts:

1) A base case return
2) a recursive function.

The base case stops the recursion, and the recursive function keeps it running. Our base case would be comment #2. Recursive case would be at comment #5.

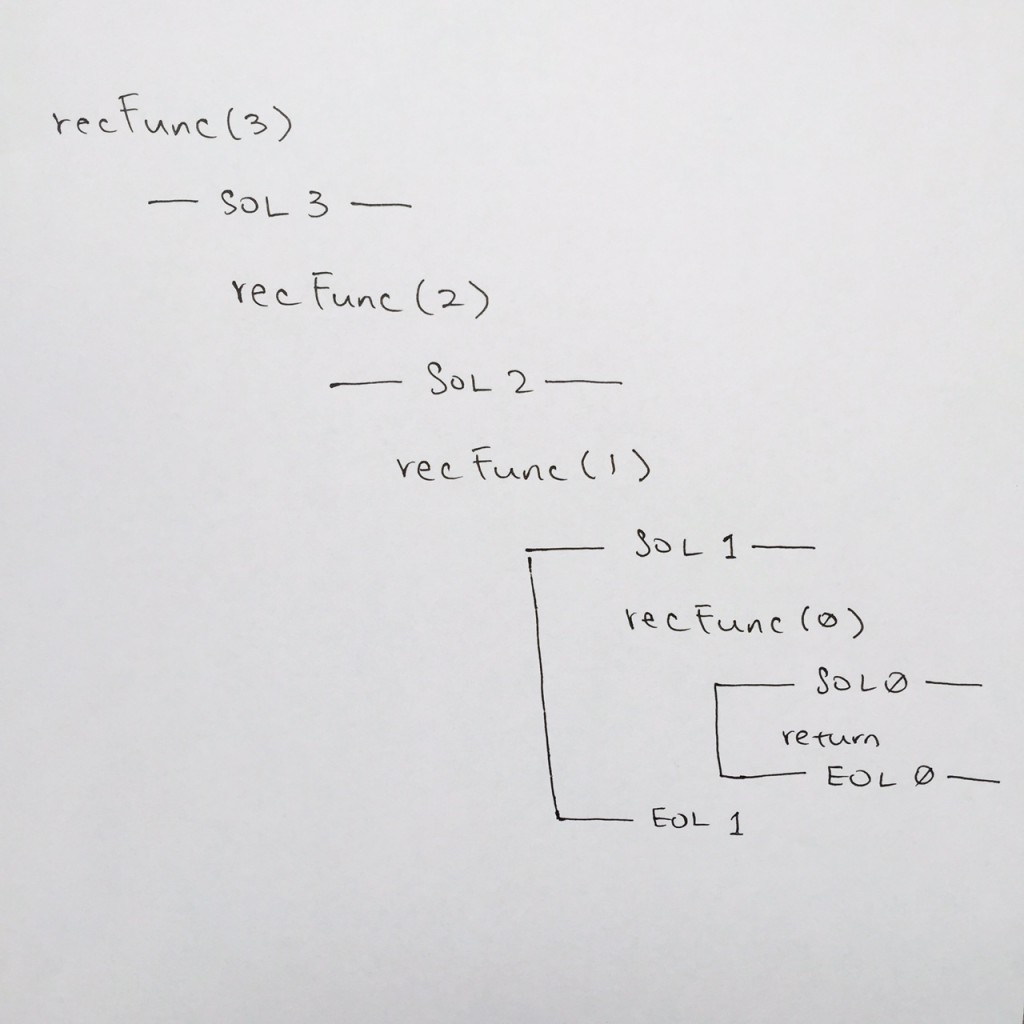
In order to properly understand how a simple recursion work, whenever a function is called, on your paper, write out the function name with its parameter. In the pictorial, you will see recFunc(3)

Then on the next line, you want say SOL (start of line). This signifies that you’ve entered the function. In the pictorial, you see —– SOL 3 ——-. Doing this will clarify that you’ve entered the frame for that function.

After the SOL for recFunc(3), we come to base case ( comment #2 ) to see if parameter n is 0.

We see that the base case is not true, so we continue down the code. We come to the recursive case with parameters n – 1 ( comment #5 ). Hence we start a new function stack.

In our paper, we skip a new line and write recFunc(2). This means we’ve entered recFunc( 2 )’s frame ( comment #1 ).

We then do —- SOL 2 —— because we’ve entered the stack for recFunc( 2 ) ( comment #1 ). We then evaluate the base case, to see if parameter n is 0. Its not so we continue on the function call recFunc(1)….

We continue on until we reach recFunc(0).

We see that the base case is true, so we go to comment #3, where you would write out the printf. Then at comment #4, we hit the return for the base case. The return means we pop the stack frame for recFunc( 0 ).

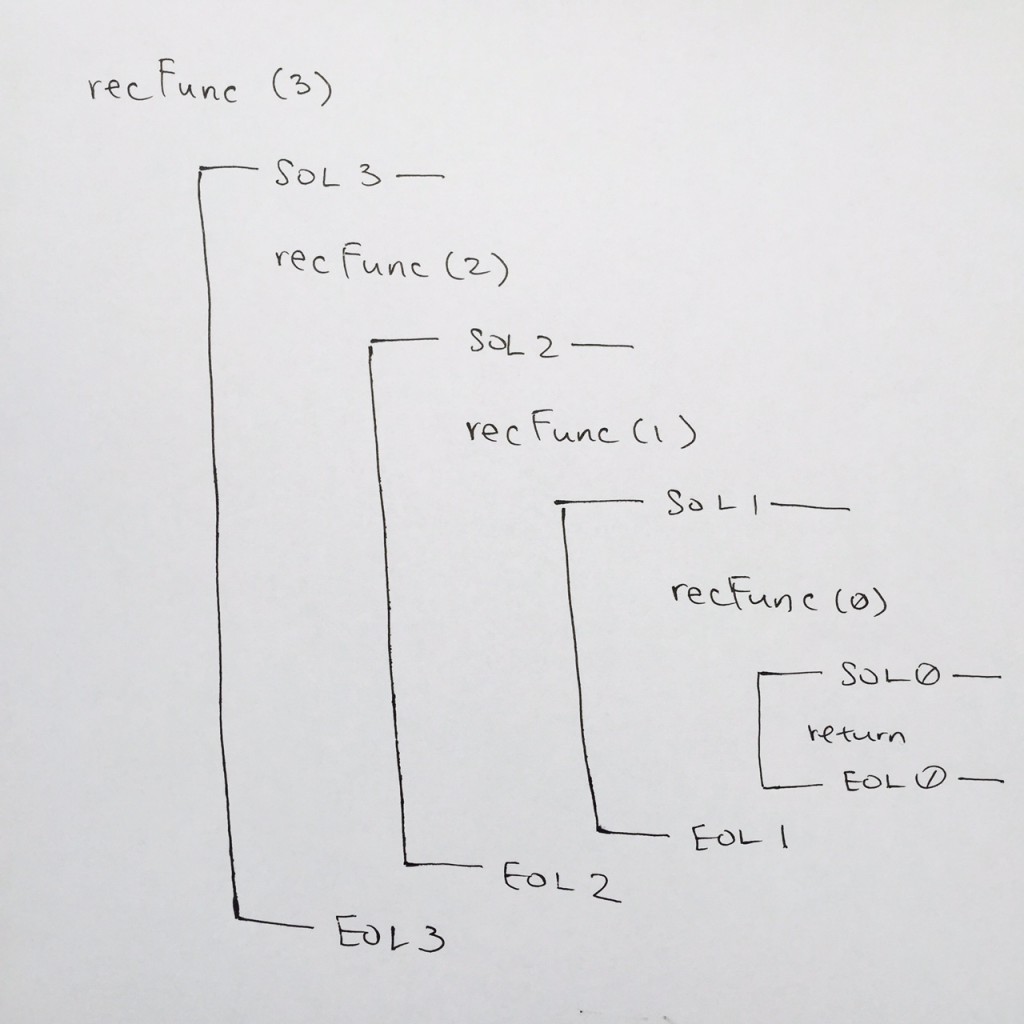
Note: Whenever a stack frame is popped, make sure you connect the lines from SOL to EOL. This can visually help you to see where the function frame has been completed.

By popping recFunc( 0 ), we continue where we left off at comment #5 of recFunc( 1 ).
We step through the code and hit EOL ( comment #6 ). So in our diagram, we connect the SOL to its EOL to show that we’ve concluded recFunc( 1 ) frame.

We pop the stack for recFunc( 1 ) and we then come to comment #5 for recFunc( 2 ). That is where we left off. We continue down, and we see EOL for recFunc( 2 ) at comment #6. We then draw the end of stack for recFunc( 2 ).

We pop the stack for recFunc(2), and we are then on recFunc(3) at comment #5. We step down, see EOL at comment #6, and in our notes, we draw the end of stack for recFunc( 3 ).

Risks of Recursion

In computing, recursion termination is when certain conditions are met and a recursive algorithm stops calling itself and begins to return values. This happens only if, with every recursive call, the recursive algorithm changes its state and moves toward the base case.

Recursive programs can fail to terminate – This error is the most common among novice programmers. Remember that your subprogram must have code that handles the termination conditions. That is, there must be some way for the subprogram to exit without calling itself again. A more difficult problem is being sure that the termination condition will actually occur.

Stack Overflow – Remember that every subprogram is a separate task that the computer must keep track of. The computer manages a list of tasks that it can maintain, but this list only has a limited amount of space. Should a recursive subprogram require many copies of itself to solve a problem, the computer may not be able to handle that many tasks, causing a system error.

Out of Memory Error – All of the subprograms we have shown here have used pass by value. That means that every time a subprogram is called it must allocate computer memory to copy the values of all the parameter variables. If a recursive subprogram has many parameters, or these parameters are memory intensive, the recursive calls can eat away at the computers memory until there is no more, causing a system error.

Sorted Linked List

November 10, 2015algorithmsadmin

download source
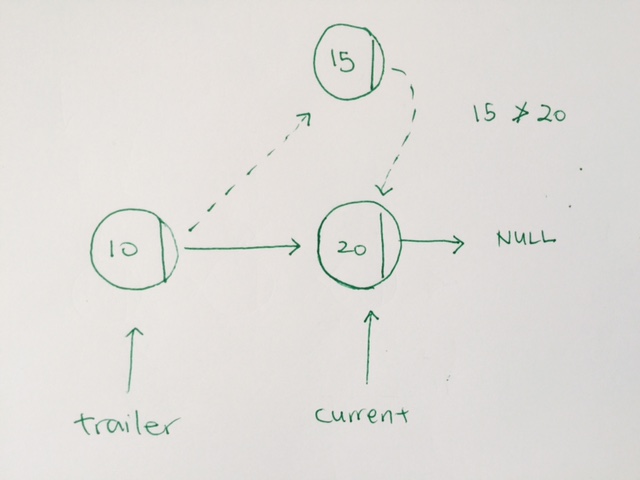
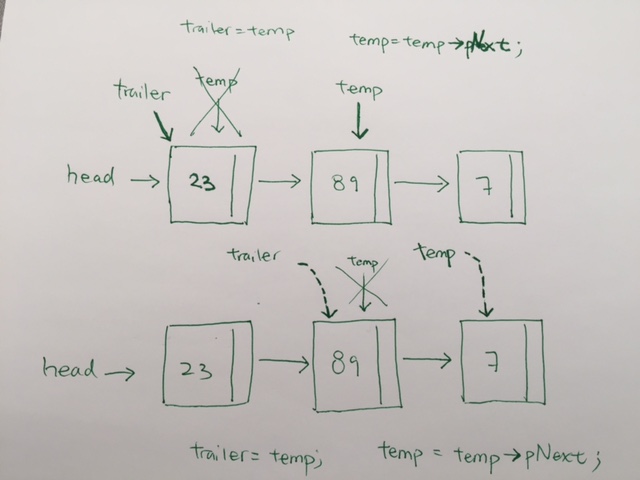
The key to understanding sorted insertion is to have 2 pointers.

One is current, the other is trailer.

While the current is not NULL, and the incoming data to be inserted is larger than the current’s data, then we move forward

We move forward by having the trailer and current move forward. Trailer take on current. Current take on current’s next.

while (current != nullptr && data > current->iData) {

//traverse forward

trailer = current;

current = current->pNext;

}

When we do find a node data, where the incoming node’s data is not larger, we stop. We have the trailer’s next point to the new node. The new node’s next take on current.

If the list empty, we simply use the first to point.

if(trailer==nullptr)

first = new Node(data, first);

else

//your data is smaller than durrent node data

trailer->pNext = new Node(data, current);

Queue Linked List

November 9, 2015algorithmsadmin

download source

Queue is First In First Out, FIFO.
This means that Nodes are processed in order. They get in line, and each node is taken care of in the order added (or received).

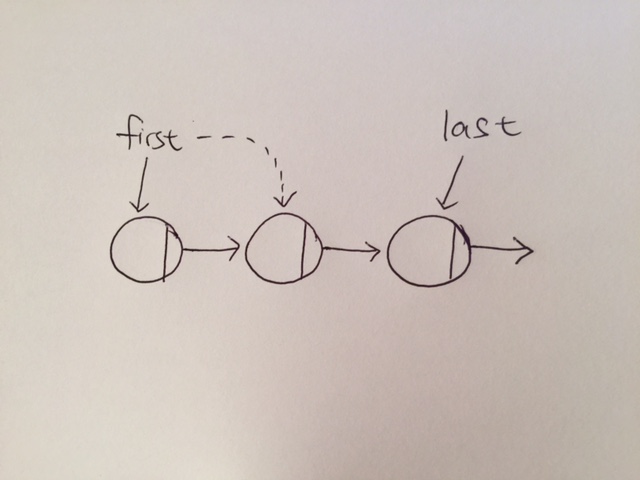
In order to do this, we have a first and a last pointer. The first pointer points to the beginning of the list, which represents the next node to be processed and removed first.

The last pointer points to the end of the list, which represents the newest node that comes in, and thus, must wait its turn for the list to process and remove it.

The first pointer points to the node TO BE processed and thus removed.

int removeFromFirst() {

if(!isEmpty()) {

Node * toRemove = first;

first = first->pNext;

int value = toRemove->iData;

toRemove->pNext = nullptr;

toRemove->iData = -1;

return value;

}

return -1;

}

The last pointer points to the position where new, incoming nodes come in.

void insertLast(int data) {

if(last == nullptr) {

first = last = new Node(data, nullptr);

}

else {

last->pNext = new Node(data, nullptr);

last = last->pNext;

}

Stack Linked List

November 8, 2015algorithmsadmin

source download

Stacked list is all about having ONE head pointer.

Pop is O(1)
Push is O(1)

The head pointer is used to add and remove.

For append:

1) We have head point to NULL in the beginning

2) First item is initialized through being supplied with values from its constructor parameters. These parameters are int data, and whatever head is pointing to.

If we’re starting out, head should be pointing to NULL. If there were previous items, then head should be pointing to the latest pushed item.

3) In the case of appending the first node, our first node’s pNext should be to what head is pointing to, which is NULL.

4) our head then re-points to the newly created Node object. Our first object as been appended.

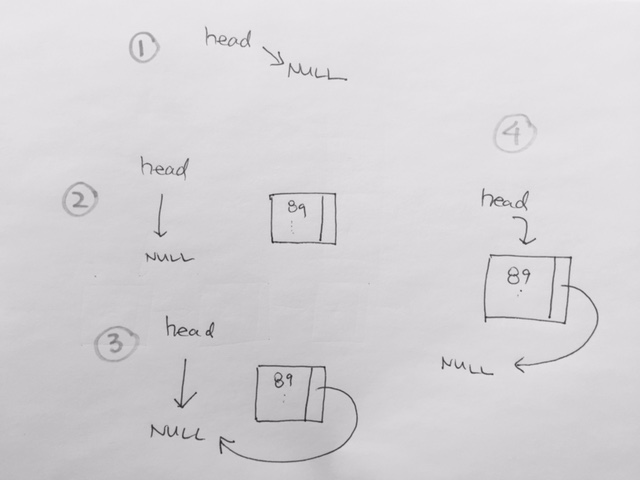
For pop, its about having a temp pointer pointing to the head, then have the head traverse 1 step forward. Then delete the object that temp is pointing to.

if(!isEmpty()) {

Node * toDelete = head;

head = head->pNext;

int toReturn = toDelete->iData;

toDelete->iData = -1;

toDelete->pNext = nullptr;

delete toDelete;

return toReturn;

}

Simple Linked List

November 7, 2015algorithmsadmin

source code

A simple linked list in C++
Basic features
Running time

Features

– add by appending
– search
– remove
– display

A linked list is a bunch of nodes ‘linked’ together by pointers. Each node has a ‘next’ pointer that points tot he next node. This is what creates the link.

First step is to create the node. The node has data and a next pointer. The next pointer should be of the same type this node because after all, the nodes are of the same type.

You’d want to have 2 constructors for the Node. An default empty one, and another where you can assign new values.

Node.h

class Node {

public:

int iData; //data

double priority;

Node * pNext; //pointer to next link

Node() {

iData = -1;

priority = -1;

pNext = nullptr;

}

Node(int data, double priority, Node * next) {

iData = data;

priority = priority;

pNext = next;

}

void displayLink() {

printf( "{ %d , %f }", iData, priority);

}

};

Node.cpp

1	#include "Node.hpp"

LinkedList.hpp

#include <stdio.h>

#include "Node.hpp"

class LinkedList {

private:

Node * head;

public:

//constructor

LinkedList() {

printf("\n --- LinkedList Constructor --- \n");

head = NULL;

}

~LinkedList()

{

printf("\n --- LinkedList Destructor --- \n");

Node * pCurrent = head;

while(pCurrent != NULL)

{

Node * toDelete = pCurrent; //the element we gon delete

pCurrent = pCurrent->pNext; //move!

delete toDelete; //delete it!

}

void append(int data, double priority);

void pop(); //O(1)

Node * find(int data); //O(n)

bool remove(int data); //O(n)

bool isEmpty(); //O(1)

void displayList(); //O(n)

};

Append

1) We have head point to NULL in the beginning

2) First item is initialized through being supplied with values from its constructor parameters. These parameters are int data, double priority, and whatever head is pointing to.

3) In the case of appending the first node, our first node’s pNext should be to what head is pointing to, which is NULL

4) our head then re-points to the newly created Node object. Our first object as been appended.

In programming, we always execute the inner most first. Then we work our way out.

1	head = new Node(data, priority, head);

The inner most is the data parameters.

First, we evaluate data to be a int. We evaluate priority to be a double. Finally, we evaluate head to point to NULL.

Then we pass these 3 values into the constructor of Node. Node object gets created with its attributes initialized. The values are initialized to , and the pNext pointer points to what head is.

Finally, when the Node object has been created, we have our head point to this Node object.

Remove

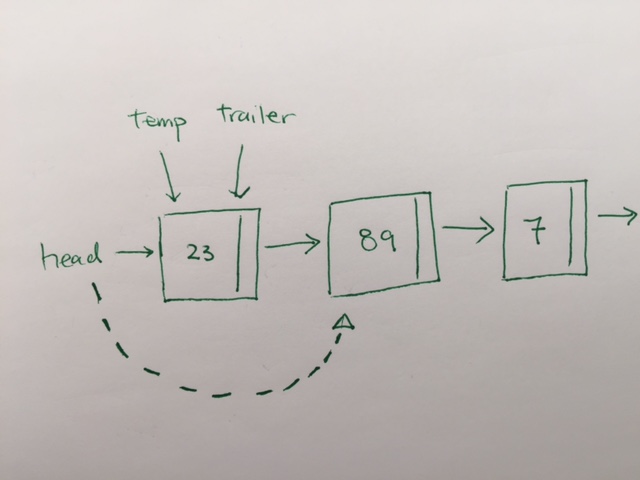
temp means the temporary node we’re on. Trailer means the pointer behind temp, so that when we remove, we can use the trailer to connect the link.

The important to notice here is

1) evaluating the first item. When temp and trailer are pointing to the same node, we’re at the first node. When we see a match, we remove the node and repoint head to the next node.

2) Moving forward to evaluate the next item involves simply checking to see if we have a match or not. If there NO match we move forward by first, pointing trailer to temp. Then have temp point to temp->next. That way, when temp has a match, then the trailer can link (the node before and after the deleted node) together.

1 2	trailer->pNext = temp->pNext; delete temp; temp = nullptr;

Running Time

Search O(n)
Delete O(n)
Append O(1)

Finding or deleting a specified item requires searching through, on the average, half the items in the list. This requires O(N) comparisons.

An array is also O(N) for these operations, but the linked list is nevertheless faster because nothing needs to be shifted when an item is inserted or removed.

The increased efficiency can be significant, especially if a copy takes much longer than a comparison.

Of course, another important advantage of linked lists over arrays is that the linked list uses exactly as much memory as it needs, and can expand to fill all available memory. The size of an array is fixed when it’s created; this usually leads to inefficiency because the array is too large, or to running out of room because the array is too small.

Vectors, which are expandable arrays, might solve this problem to some extent, but they usually expand in fixed-sized increments (such as doubling the size of the array whenever it’s about to overflow). This use of memory is still not as efficient as a linked list.

Stacks and Queues

November 5, 2015algorithmsadmin

In an array, any item can be accessed, either immediately through its index, or by searching through the sequence of cells until its found.

In stacks and queues, however, access is restricted. Only one item can be read or removed at a given time.

Their interface is designed to enforce this restricted access. Theoretically, access to other items are not allowed.

Stacks and Queues are abstract by nature. What I mean by that is that they are defined by their interface. Their underlying workings can be different. For example, A stack may have push, pop, view, etc as its interface. But the underlying mechanism may be an array of a linked list.

Some ways to use Stacks

Reverse a word

Use a stack to reverse a word. When a string of word comes in, push each character into your stack. Then pop the stack onto an empty string, and you will then have the word reversed.

Delimiter Matching

Another common use for stacks is to parse certain kinds of text strings. The delimiters are (, ), [, ], {, }…etc.

You have an empty stack

You have a string say “a{b(c[d]e)f}”

read “a”
“a” != delimiter, go on.
Stack:

read “{”
“{” is opening delimiter, push onto stack.
Stack: {

read “b”
“b” != delimiter, go on.
Stack: {

read “(”
“(” is opening delimiter, push onto stack.
Stack: { (

read “c”
“c” != delimiter, go on.
Stack: { (

read “[”
“[” is opening delimiter, push onto stack.
Stack: { ( [

read “d”
“d” != delimiter, go on.
Stack: { ( [

read “]”
“[” is closing delimiter, pop from stack.
Stack: { (

read “e”
“e” != delimiter, go on.
Stack: { (

read “)”
“)” is closing delimiter, pop from stack.
Stack: {

read “f”
“f” != delimiter, go on.
Stack: {

read “}”
“}” is closing delimiter, pop from stack.
Stack:

Using Queues

Queues are first in first out.

In Arrays, when we insert, we just push onto the array, which is O(1).
When we delete, we remove the 0th element, then push all the elements down, which is O(n).

In linked list, we have head and tail pointer. This would make both adding and removing O(1).

However, search and delete would be O(n) because on average, it takes n/2 where n is number of items. T = k * (n/2) where constants are included T = n. In regards to how fast it is to the number of items, we have T = O(n)

priority queues

0 is highest priority, a larger number means a lower priority.

Thus, when we insert an item, we start at the very end of the array. Use a for loop back to 0th index, and see if the new element is larger than the element at the index.

The new element being a larger element means it has a lower priority. If it is, we shift the array element up. We keep doing this until our priority is properly inserted. Having the smallest number mean we have a higher priority, thus, we append the element at the top.

When we delete, we simply pop the top element.

Big O notation basics

November 4, 2015algorithmsadmin

http://www.codenlearn.com/2011/07/understanding-algorithm-complexity.html
https://www.quora.com/How-would-you-explain-O-log-n-in-algorithms-to-1st-year-undergrad-student

Hardware execution time

Let’s say an assignment

1	array[length++] = 13

is one step.

This requires the same amount of time no matter how big the length of array is. We can say that time, T, to insert an item into an unsorted array is a constant K:

T = K

In detail, the actual time (in ms or whatever unit of measure) is required by the insertion is:

related to the speed of the microprocessor
how efficiently the compiler has generated the program code
..other factors

Linear Search

The number of comparisons that must be made to find a specified item is, ON AVERAGE, half of the total number of items. Hence, if N is the total number of items, the search time T is

N = number of items
T = time
K = execution time of hardware

T = K * (N / 2)

For a handier formula, we can lump the 1/2 into the K, because we are dealing with constant numbers. Hence we can say a constant K is
some constant K which represents execution time of the hardware divided by 2.

Hence, T = K * N

Time = hardware execution time * Number of items

The reason why we do this is because, we’re not interested in the actual execution time. We’re just interested in how fast the algorithm is running IN ACCORDANCE TO THE NUMBER OF ELEMENTS N.

Thus, whatever execution time is for the particular processor and compiler at the time does not matter to us. Whether its a 333mhz processor or a 3ghz processor, it doesn’t matter.

We just lump that constant numeric together and pull out the number of elements N SO THAT we can convey how running times are affected by the number of items.

This says that average linear search times are proportional so the size of the array.

For example,

In an unordered array, Search takes O(N) time because you need to go through N/2 elements on average. Multiple that that by processing time constant K time T = (N/2) * K = K * N = O(N) where we don’t care about literal processing time of K.

In an unordered array, Deletion takes O(N) time because once you use Search to find the element to delete, you still need to shift elements down to fill the empty spot. On average its N/2 elements that you need to shift down. Multiple that by processing time constant K time T = (N/2) * K = K * N = O(N) where we don’t care about processing time of K.

Binary Searching

T is time
K is hardware execution time
N is number of items

T = K * log (base 2) N

But because whether we’re dealing with binary three, or tinery tree, or whatever, base 2, base 3…etc is simply a constant numeric. i.e lay out a base 2 framework and a base 10 framework, their difference is 3.322. That’s a numeric that we can include into the constant K.

Hence, T = K * log N.

Eliminating the Constant K for Big O

When comparing algorithms you don’t really care about the particular microprocessor chip or compiler, all you want to compare is how T changes for different values of N. Therefore, the constant isn’t needed.

Big O notation uses the uppercase letter O, which you can think of as meaning “order of”. In Big O notation, we would say that a linear search takes O(N) time, binary search takes O(log N) time. Insertion into an unordered array takes O(1), or constant time.

The idea in Big O notation isn’t to give an actual figure for running time, but to convey how running times are affected by the number of items.

Log(n)

In the case of binary search, you are trying to find the maximum number of iterations, and therefore the maximum number of times the search space can be split in half.

This is accomplished by dividing the size of the search space n, by 2 repeatedly until you get to 1 number.

Let’s give the number of times you need to divide n by 2 the label x. Since dividing by 2 x times is equivalent to dividing by 2^x, you end up having to solve for this equation:

n total number of items
x number of times you need to divide by 2 to get the result 1

n / 2^x = 1

x is the number of times you can split a space of size n in half before it is narrowed down to size 1.
The solution to this equation be found by taking the logarithm of both sides:

2^x = n

by log mathematical inductions….

log (2^x) = log (n^1)

x log 2 = 1 * log n

x = log ( n ) / log ( 2 ) = log base 2 (n)

Hence

x = log base 2 (n)

means that given n numbers, x is the number of times we split those n numbers in half, in order to get a result of 1.

Core Data #3 – sibling Main/Private MOC on a PSC

November 2, 2015iOScore dataadmin

CoreData Stack #3 xCode 7.3

ref – http://blog.chadwilken.com/core-data-concurrency/
http://stackoverflow.com/questions/30089401/core-data-should-i-be-fetching-objects-from-the-parent-context-or-does-the-chil
https://github.com/skandragon/CoreDataMultipleContexts

https://medium.com/bpxl-craft/thoughts-on-core-data-stack-configurations-b24b0ea275f3#.vml9s629s

In iOS 5, Apple introduced

1) parent/child contests – settings a context as a child to a parent context is that whenever the child saves, it doesn’t persist its changes to disk. It simply updates it own context via a NSManagedObjectContextDidSaveNotification message. Instead, it pushes its changes up to its parent so that the parent can save it.
2) concurrency queue that is tied to a context. It guarantees that if you execute your code block using that context, it will use execute your code block on its assigned queue

Thus, we can use parent/child contexts and concurrency queue to set up our Core Data Stack.

Say we create a parent context. It will act as the app’s Task Master. Its children will push their changes up so that the task master will and executes them in a background queue.

When creating this Task Master context, we init it with macro NSPrivateQueueConcurrencyType to let it know that the queue is a private one. Because its a private queue, the threads used to run the tasks in this private queue will be executed in the background.

@interface CoreDataStack : NSObject

{

}

+(instancetype) defaultStack; //instantiations of self MUST accesses this class method.

//no other instantiations of this method is possible. Thus we ensure 1 entry point.

//background context

@property (readonly, strong, nonatomic) NSManagedObjectContext * privateQueueManagedObjectContext;

...

@end

@interface CoreDataStack ()

@property (nonatomic, strong) NSHashTable * contextDirectory;

@end

@implementation CoreStackData

@synthesize contextDirectory; //to keep storage of all the temporary contexts

//private queue context does job in the background

@synthesize privateQueueManagedObjectContext = _privateQueueManagedObjectContext;

....

- (NSManagedObjectContext *)privateQueueManagedObjectContext {

if (_privateQueueManagedObjectContext != nil) {

return _privateQueueManagedObjectContext;

}

NSPersistentStoreCoordinator *coordinator = [self persistentStoreCoordinator];

if (!coordinator) {

return nil;

}

_privateQueueManagedObjectContext = [[NSManagedObjectContext alloc]

initWithConcurrencyType: NSPrivateQueueConcurrencyType];

[_privateQueueManagedObjectContext setPersistentStoreCoordinator:coordinator];

_privateQueueManagedObjectContext.mergePolicy = NSMergeByPropertyObjectTrumpMergePolicy;

return _privateQueueManagedObjectContext;

}

.....

@end

Now, let’s a child context. We we create a temporary MOC who’s parent context is our Task Master.

- (NSManagedObjectContext *)createBackgroundContext

{

NSManagedObjectContext * context = [[NSManagedObjectContext alloc] initWithConcurrencyType:NSPrivateQueueConcurrencyType];

context.parentContext = self.privateQueueManagedObjectContext;

context.mergePolicy = NSMergeByPropertyObjectTrumpMergePolicy;

//We use this contextDirectory to decide if we should merge the changes into the mainQueueManagedObjectContext

//by ensuring that the context triggering the notification exists in the directory as used in handleMOCDidSaveNotification.

[self.contextDirectory addObject:context]; //weak reference

return context;

}

Notice its parentContext assigned to our Task Master.

This implies that whenever our temporary MOCs finish their tasks, (whether its getting data from the net or reading in loads of data from somewhere or whatever task that takes quite a bit of time) and that we call MOC’s save,
this does 2 things:

1) save sends the NSManagedObjectContextDidSaveNotification message, and thus our Notification center observes. We go to handleMOCDidSaveNotification method where we call a method for the parentContext (task master) to do the save.

2) The background context’s changes are pushed into its parent context (task master).

Here is the handler that handles all name:NSManagedObjectContextDidSaveNotification message triggered by our child temporary MOCs.

//Whenever the <notifiation> NSManagedObjectContextDidSaveNotification from <object> is sent, then we call the selector method

[[NSNotificationCenter defaultCenter] addObserver:self

selector:@selector(handleMOCDidSaveNotification:)

name:NSManagedObjectContextDidSaveNotification

object: nil];

where handleMOCDidSaveNotification is:

- (void)handleMOCDidSaveNotification:(NSNotification *)notification {

NSManagedObjectContext *context = [notification object];

NSLog(@"handleMOCDidSaveNotification - %p", context);

//because we already said that if the main context sends a NSManagedObjectContextDidSaveNotification, then go to saveMasterContext,

//when we implement handleMOCDidSaveNotification, we have to be careful to avoid the ui context. We ONLY want to take care of

//worker context. If its not a worker context OR if its the main UI context, we simply return.

if (![self.contextDirectory containsObject:context] || context == self.mainQueueManagedObjectContext)

{

NSLog(@"%p is not a temp worker OR its a main queue context! Let's not touch it.....", context);

return;

}

NSLog(@"handleMOCDidSaveNotification - background temp worker %p trigged this method...", context);

//it is a temp worker context...so we have the main main UI context, merge with its changes...

//it merges in the changes to the main UI context inside a performBlockAndWait call, ensuring it happens on the correct queue.

[self.mainQueueManagedObjectContext performBlockAndWait:^{

NSLog(@"handleMOCDidSaveNotification - merge changes to main UI context");

[self.mainQueueManagedObjectContext mergeChangesFromContextDidSaveNotification:notification];

//notice its just a merge. There is no save

}];

NSLog(@"background MOC calls Parent private Context to save");

//Once this finishes we go ahead and call saveMasterContext which in fact persists the changes to disk using the privateQueueManagedObjectContext.

[self saveMasterContext];

}

//whenever a worker context saves, it first merges with the main UI context, then it comes here for

//the private context to do its saves

- (void)saveMasterContext {

NSLog(@"saveMasterContext - PRIVATE QUEUE SAVING....");

[self.privateQueueManagedObjectContext performBlockAndWait:^{

NSManagedObjectContext * privateQueueMOC = self.privateQueueManagedObjectContext;

if(privateQueueMOC != nil) {

NSError *error = nil;

if ([privateQueueMOC hasChanges] && ![privateQueueMOC save:&error]) //if the private MOC has changes and saved with error

{

NSLog(@"Unresolved error %@, %@", error, [error userInfo]);

abort();

}

else {

NSLog(@"private MOC has changes AND saved with no problem");

}

}];

}

In handleMOCDidSaveNotification, we ignore other context, we take care of these temporary MOCs only. We RETURN and do nothing iff the temp MOCs are NOT tracked in our NSHashTable directory, or if its the UI context.

If the temp MOCs ARE tracked, that means they are temp MOCs, and we go ahead merge our temp MOCs with the UI MOC. We merge our changes with the UI MOC, because the UI MOC is not a parent context of the temp MOCs. The UI MOC is a separate entity.

When a MOC saves, its changes are pushed into its parent context. These however are not immediately written to disk. We write to the disk, after the background MOC saves, sends the NSManagedObjectContextDidSaveNotification notification, we go into handleMOCDidSaveNotification, and in the method saveMasterContext. saveMasterContext saves our parent private context, thus making it write to disk, and if it takes a long, its ok because its a private background queue.

http://stackoverflow.com/questions/30089401/core-data-should-i-be-fetching-objects-from-the-parent-context-or-does-the-chil

In short,

To clear up the confusion: after creating the child context from a parent context, that child context has the same “state” as the parent. Only if the two contexts do different things (create, modify, delete objects) the content of the two contexts will diverge.

So for your setup, proceed as follows:

create the child context
do the work you want to do (modifying or creating objects from the downloaded data),
save the child context
At this stage, nothing is saved to the persistent store yet. With the child save, the changes are just “pushed up” to the parent context. You can now

save the parent context
to write the new data to the persistent store. Then

update your UI,
best via notifications (e.g. the NSManagedObjectContextDidSaveNotification).