Memoization Components

ref –

https://medium.com/@rossbulat/how-to-memoize-in-react-3d20cbcd2b6e
https://dmitripavlutin.com/use-react-memo-wisely/
https://medium.com/@reallygordon/implementing-memoization-in-javascript-5d140bb04166
https://blog.bitsrc.io/improve-react-app-performance-through-memoization-cd651f561f66
https://reactgo.com/react-usememo-example/

Memoization is the process of caching a result of inputs linearly related to its output, so when the input is requested the output is returned from the cache instantaneously.

Memoization is an optimization technique used to primarily speed up programs by storing the results of expensive function calls and returning the cached results when the same inputs occur again.

Say we have a simple function that calculates the Fibonacci number like so:

// original function

function recursiveFib(n) {

if (n <= 1) {return n}

return recursiveFib(n-1) + recursiveFib(n-2)

}

Say we put in a parameter of 5. We’d draw out a three of how our recursive calls would go. Where as we drill down to where parameter n is 0 or 1. That is the base case
where we return their respective numbers

recursiveFib(5)

recursiveFib(4) + recursiveFib(3)

recursiveFib(3) + recursiveFib(2) recursiveFib(2) + recursiveFib(1)

recursiveFib(2) + recursiveFib(1) recursiveFib(1) + recursiveFib(0) recursiveFib(1) + recursive(0) recursiveFib(1) + recursiveFib(0)

As you can see, we make calls to recursiveFib(2) three times. recursiveFib(1) five times. And recursiveFib(3) two times.

This is a lot of recalculations. The concept of memoization is to store them in a cache so that we only calculate each parameter once. Any future calls would simply take O(1) time and we can access the results immediately.

Here, we create a function that contains a key/value cache with a simple JS literal object called memo. Then we return our fib function from above. We put it just below memo. Since we return this function to elsewhere, our fib function can access memo via closure.

Before ANY kind of recursive calculation is done, we first comb through our memo to see if the n exists. If it exists, it means we have already processed it. We just access. If it’s not found, we move on to calculate the fib number for n. The recursion is exactly the same. Except that we make sure to put the result into our memo cache when done.

const memoFib = function() {

console.log('returning to you a fib function that memoized')

let memo = {

} // access by closure

// return the fib function

// access our key/value table via closure

return function fib(n) {

if (n in memo) {

console.log(`access cache of ${memo[n]} from ${n.toString(10)}`)

return memo[n.toString(10)]

}

else {

if (n <= 1) { // assign 0 to 0, 1 to 1

memo[n.toString(10)] = n

console.log(`stored ${n} to ` + memo[n.toString(10)]);

}

else {

let result = fib(n - 1) + fib(n - 2) ;

memo[n.toString(10)] = result;

console.log(`stored ${result} at ${n.toString(10)}`)

}

return memo[n.toString(10)]

}

Going through the details

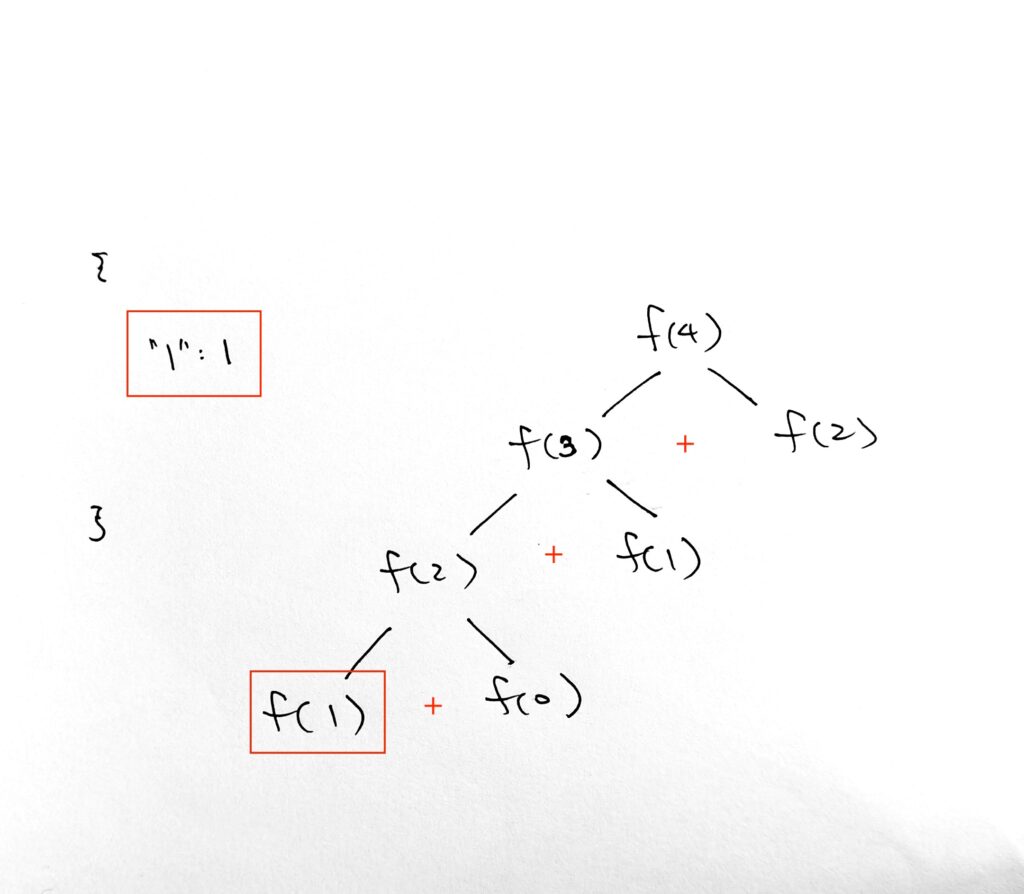
We start off by processing fib(5), which is fib(4) + fib(3)

By order, we then recurse fib(4), which is fib(3) + fib(2)

By order, we then recurse fib(3), which is fib(2) + fib(1)

By order, we then recurse fib(2), which is fib(1) + fib(0)

By order, we then recurse fib(1), which is the end case.
log “stored 1 to 1”
So we create new cache value 1 for key 1

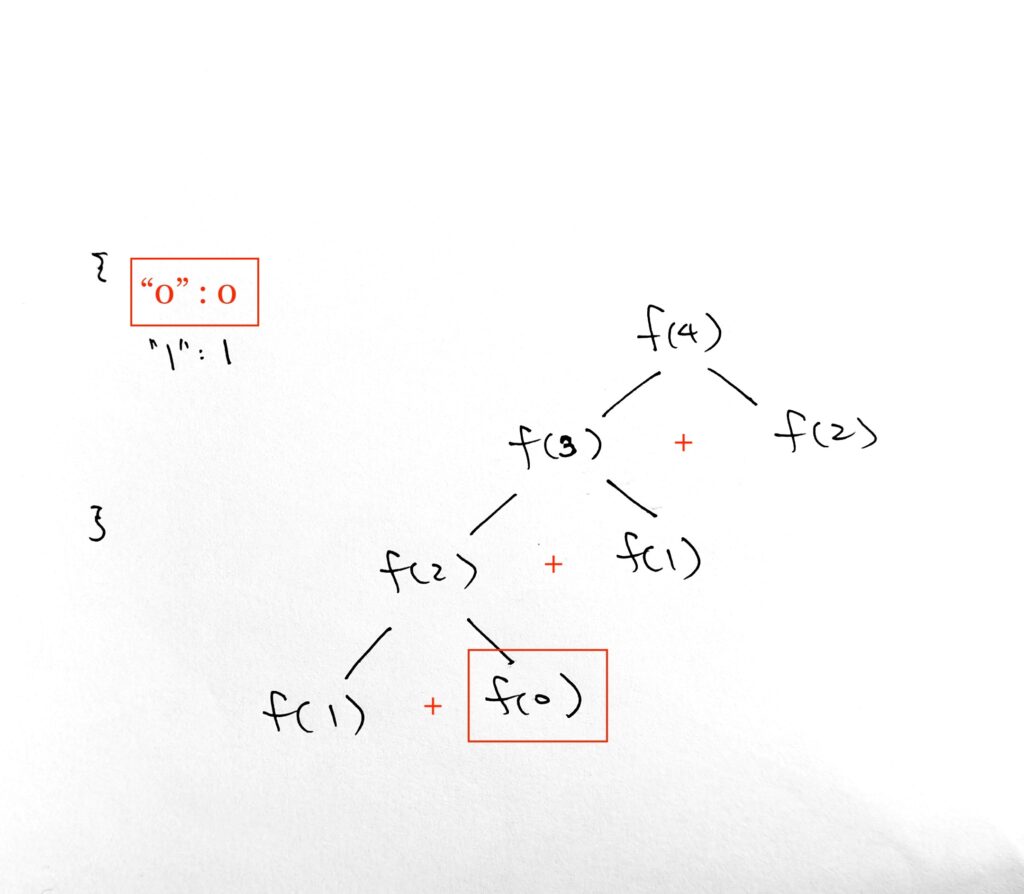
Moving on to fib(0), its an end case. So we create new cache value 0 for key 0
log “stored 0 to 0”

The addition of both gives fib(2) = 1 + 0.
We create new cache value 1 for key 2.

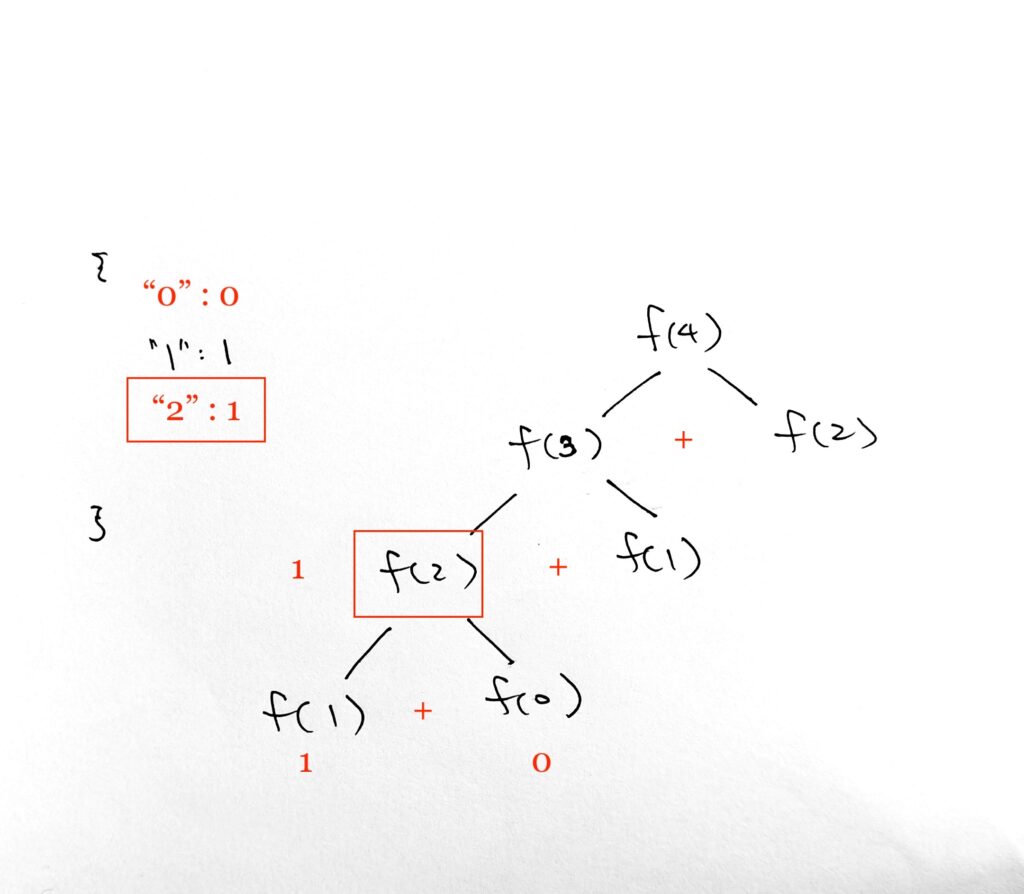
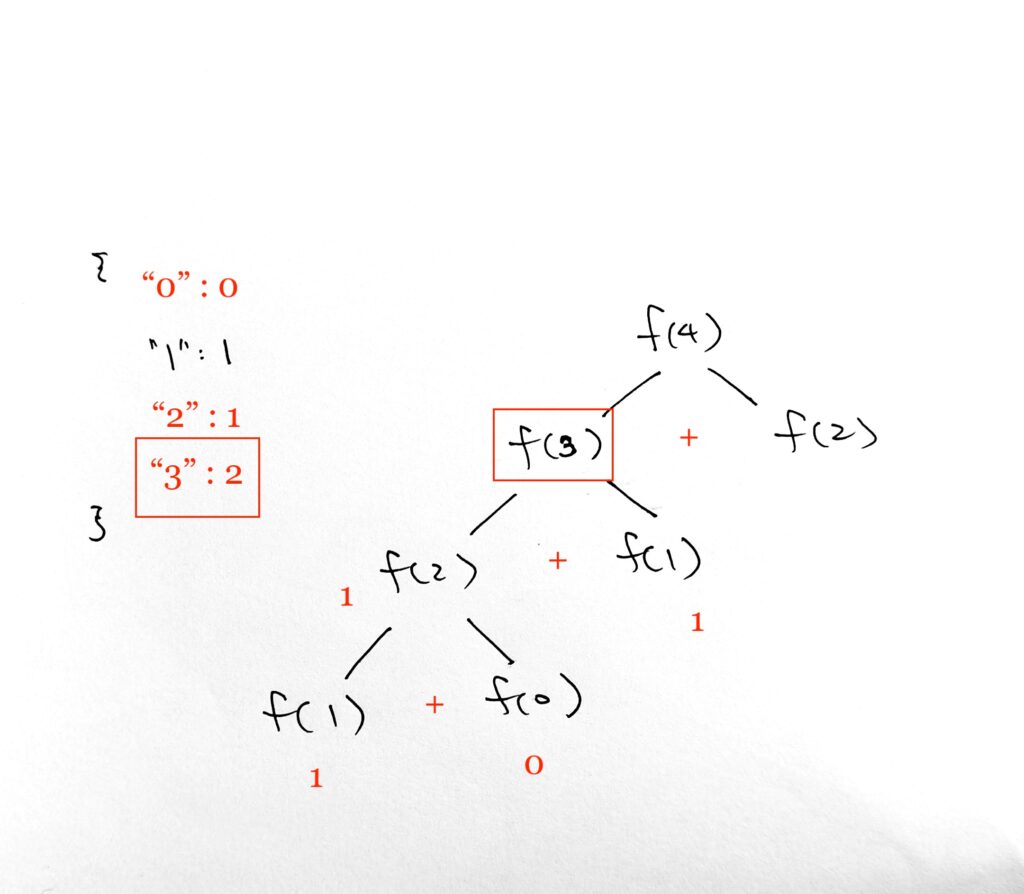
On fib(3) = fib(2) + fib(1), we move on to fib(1)
Notice that we have a key/value in our cache for key 1. Hence we simply access it. This saves us calculation and processing time.

We then have fib(3) = 1 + 1 = 2.
We create cache value 2 for key 3.

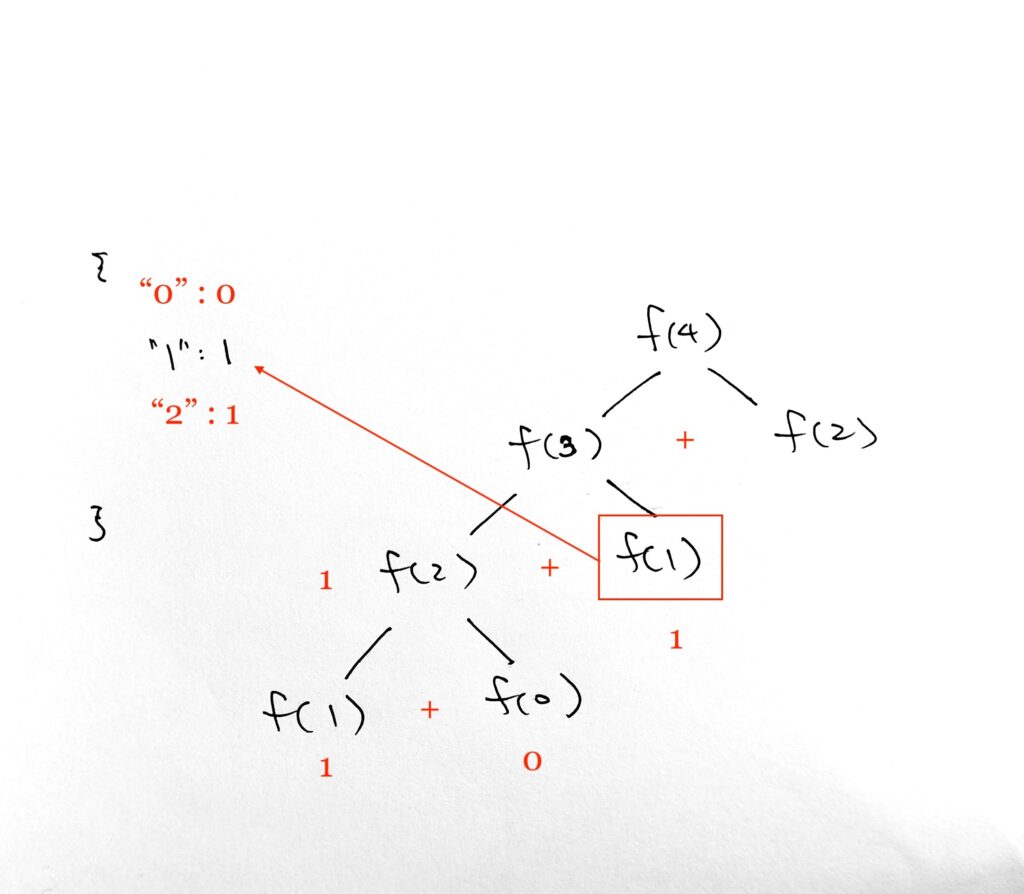
On fib(4) = fib(3) + fib(2), we move on to fib(2). Notice again that key 2 already exists. We can save time again and just get the cache.

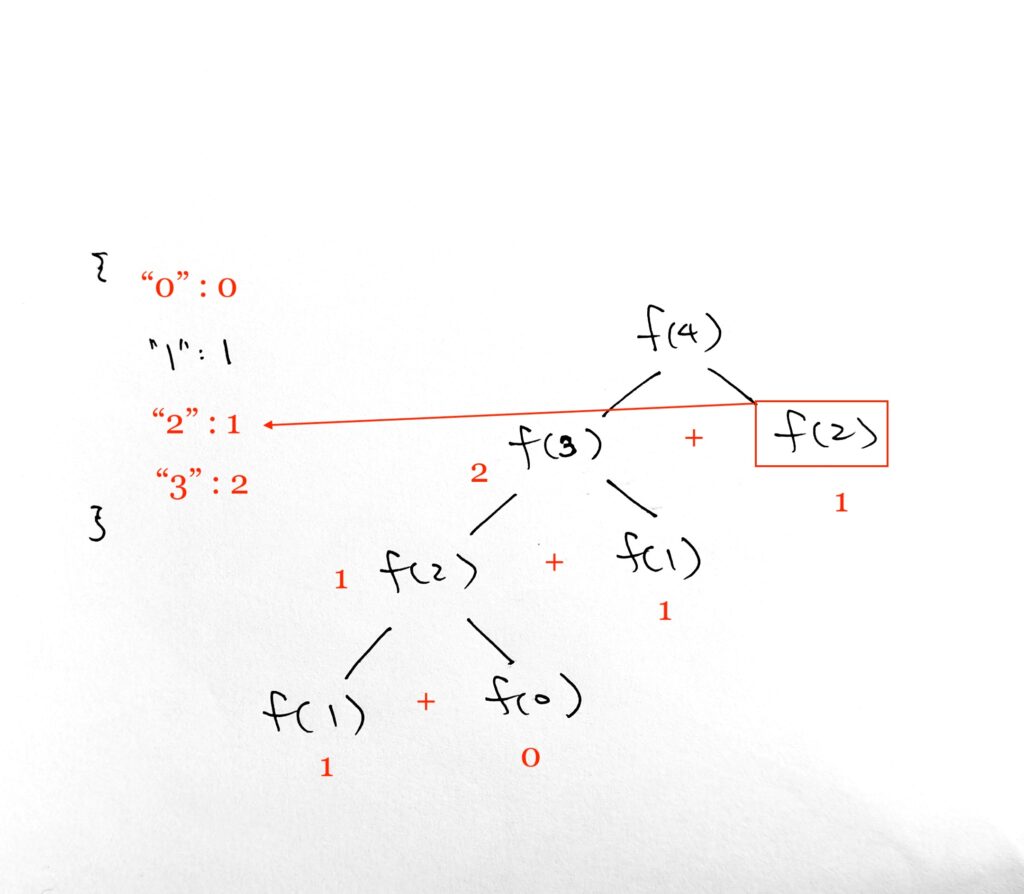
Finally, fib(4) = 2 + 1 = 3. We insert cache value 3 for key 4.

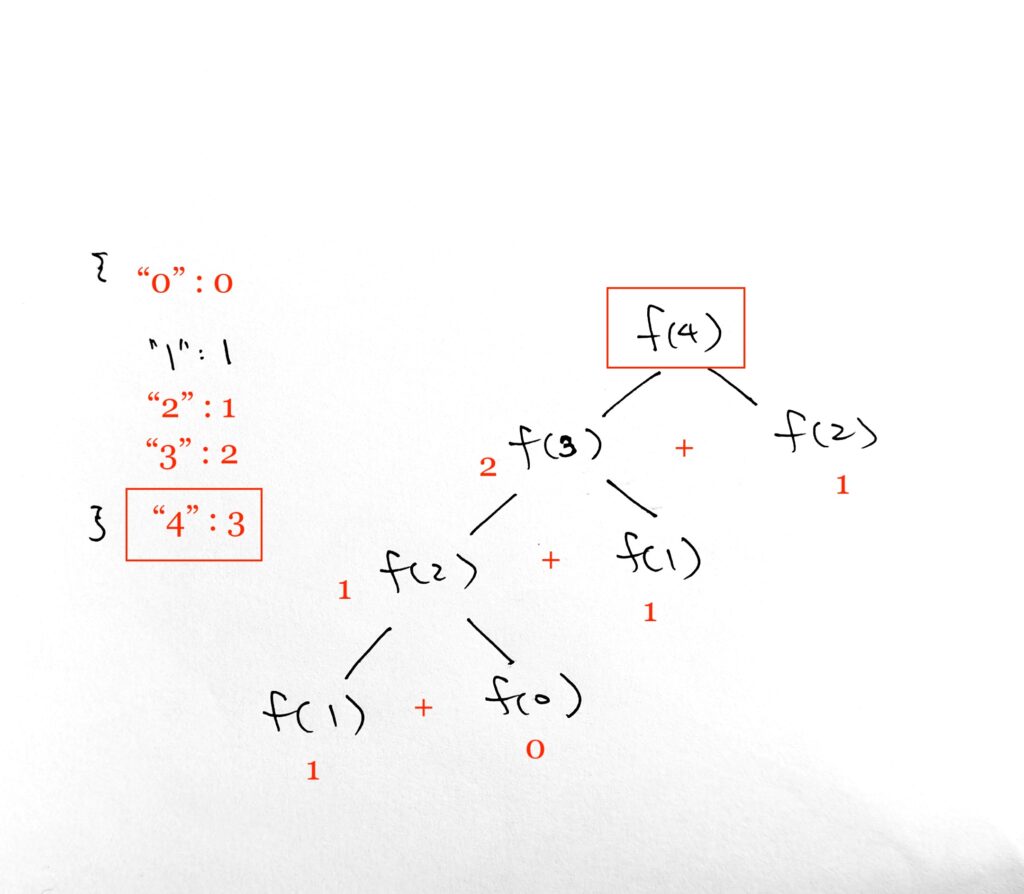
– Fibonacci recursive functions are a “pure” functions — that is, the same input value will always return the same output. This is a necessary condition for using memoization, as our cache needs to remember ONE SINGLE return values for the inputs.

– Memoization trades time for space — we must create a space in our cache for every input needed to calculate our result.

We first create a state with input 0.
We then create a button that handles an input.
In the input, we put the # of times we want to repeat the input being changed to 8.

you’ll notice as we use setTimeout to change it the state 3 times to the value 8. The render function gets called 3 times, even though the state.input is always 8.

class App extends React.Component {

constructor() {

super();

this.state = {

input: 0

}

this.recursiveFib = n => {

if (n <= 1) {

return n

}

let result = this.recursiveFib(n-1) + this.recursiveFib(n-2);

return result;

}

this.handleInput = this.handleInput.bind(this);

}

// prototype functions

handleInput = evt => {

console.log('changed input to', evt.target.value)

for (let i =0 ; i < evt.target.value; i++) {

// we loop n times and set the state to 8

setTimeout(

() => {

console.log('called setState');

this.setState({ input: 8 })

1000*i

);

}

render() {

console.log('-- render --');

const { input } = this.state;

console.log('input', input);

return (

<h2> {this.recursiveFib(8) } </h2>

</header>

</div>

);

}

output:

input to 3
called setState
— render —
input 8
called setState
— render —
input 8
called setState
— render —
input 8

Improve with PureComponent

If we were to extend PureComponent, it actually shallow checks to see if the previous prop/state is the same as the current prop/state.
If its the same, we won’t re-render.

Simply change this line of code:

1	class App extends React.Component {

1	class App extends React.PureComponent {

result:

changed input to 5

called setState

-- render --

input 8

(4) called setState

Therefore PureComponent improves your performance.

Improving Performance with Memoization

Let’s write a simple function where we wait for some seconds.

In your fib function, right before you return a value, let’s simulate that the calculation takes 1 second.

function wait(milliseconds=0) {

console.log('waiting ' + milliseconds/1000 + ' seconds');

var now = Date.now()

var end = now + milliseconds

while (now < end) {

now = Date.now()

}

So we put wait(1000) in front of all returns in our recursiveFib.

this.recursiveFib = n => {

if (n <= 1) {

wait(1000);

return n

}

let result = this.recursiveFib(n-1) + this.recursiveFib(n-2);

wait(1000);

return result;

}

Let’s put recursiveFib in our render. Whenever we input a number, it calls setState in the input, and thus will call our render.

render() {

console.log('-- render --');

const { input } = this.state;

console.log('rendering fibonacii input of ', input);

return (

<h2> {this.recursiveFib(input) } </h2>

</header>

</div>

);

}

When we run all the code together, you’ll notice that it it gets stuck processing all the simulated processing time (of 1 sec) before the render.
So this is to simply show that if we have some calculations that take up a lot of time, and its hurting our render time, how do we further improve performance with memoization?

class App extends React.PureComponent {

constructor() {

super();

this.state = {

input: 0

}

this.recursiveFib = n => {

if (n <= 1) {

wait(1000);

return n

}

let result = this.recursiveFib(n-1) + this.recursiveFib(n-2);

wait(1000);

return result;

}

this.handleInput = this.handleInput.bind(this);

}

// prototype functions

handleInput = evt => {

console.log('changed input to: ', evt.target.value);

this.setState({ input: evt.target.value })

}

render() {

console.log('-- render --');

const { input } = this.state;

console.log('rendering fibonacii input of ', input);

return (

<h2> {this.recursiveFib(input) } </h2>

</header>

</div>

);

}

Because every single node must be calculated from scratch, we must calculate for a total of 9 nodes. If each node takes 1 second, then it takes 9 seconds.

output:
changed input to: 4
— render —
rendering fibonacii input of 4
waiting 1 seconds
waiting 1 seconds
waiting 1 seconds
waiting 1 seconds
waiting 1 seconds
waiting 1 seconds
waiting 1 seconds
waiting 1 seconds
waiting 1 seconds

So total processing time for standard fib is 9 seconds.

Let’s change by using our memoizationFib.

this.memoFib= () => {

console.log('returning to you a fib function that memoized')

let memo = { } // access by closure

return function fib(n) {

if (n in memo) {

wait(1000);

return memo[n.toString(10)]

}

else {

if (n <= 1) { // assign 0 to 0, 1 to 1

memo[n.toString(10)] = n

}

else {

let result = fib(n - 1) + fib(n - 2) ;

memo[n.toString(10)] = result;

}

wait(1000);

return memo[n.toString(10)]

}

Now instead of 9 seconds, we simply wait 7 seconds.

output:

f(4)
App.js:106 f(3)
App.js:106 f(2)
App.js:106 f(1)
App.js:65 waiting 1 seconds
App.js:106 f(0)
App.js:65 waiting 1 seconds
App.js:65 waiting 1 seconds
App.js:106 f(1)
App.js:65 waiting 1 seconds
App.js:65 waiting 1 seconds
App.js:106 f(2)
App.js:65 waiting 1 seconds
App.js:65 waiting 1 seconds

The differences get bigger as the recursion increases.

For standard Fib(9) when you calculate everything, its 109 seconds.
Whereas if you use memoization, and save calculations, it only takes 17 seconds. This is because you avoid re-calculating subtrees.