Longest Prefix Suffix (lps)
Longest Prefix Suffix indicates how many matching prefix/suffix strings there are.
In other words, it tell us how many prefix matches we have in the pattern’s current character, which acts as a suffix.
For example, in the example below:
01234 (index)
abcya (pattern)
00001 (lps)
at index 4, we have lps of 1. The prefix is ‘a’. The suffix is ‘a’.
[a]bcy[a]
going further, lps[5] is 2, because the prefix is ‘ab’. The suffix is ‘ab’.
[ab]cy[ab]
012345 (index)
abcyab (pattern)
000012 (lps)
at index 6, we have 3.
0123456 (index)
abcyabc (pattern)
0000123 (lps)
The prefix is ‘abc’. The suffix is ‘abc’.
[abc]y[abc]
No match situation
012 (index)
abc (pattern)
000 (lps)
lps[0] defaults to 0 because there is no suffix to compare with a prefix.
Then when we get ab, the ‘a’ is the prefix, and the ‘b’ is the suffix.
We compare them, they do not match. Thus, lps[1] is 0.
Then we compare a with c. Where ‘a’ is the prefix, and the ‘c’ is the suffix.
They do not match, thus, lps[2] = 0.
How to calculate the LPS array
The source code is like so:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
kmp_LPS(pattern, patternLength, lps) { let j = 0; let i = 1; lps[0] = 0; // lps[0] is always 0 while (i < patternLength) { let iPatternCh = pattern[i]; let jPatternCh = pattern[j]; if (iPatternCh == jPatternCh) { j++; lps[i] = j; i++; } else { if (j!= 0) { j = lps[j - 1]; } else { lps[i] = j; i++; } } } console.log(lps); return lps; } |
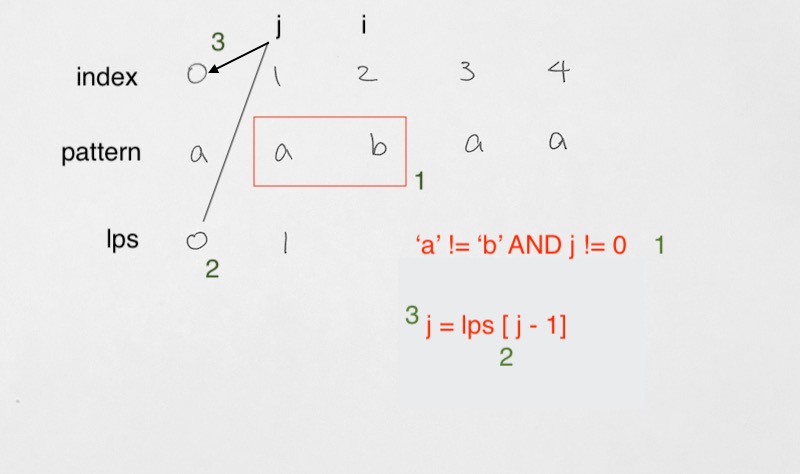
Let’s go through it on a pattern of a a b a a.
We start off j = 0, i = 1. We need to have a parallel matching scheme. Thus, both index will be going down the array in a parallel fashion.
Note that lps[0] is always 0 because at index 0, we only have 1 character.
When going down the array in parallel, we come to 2 situation:
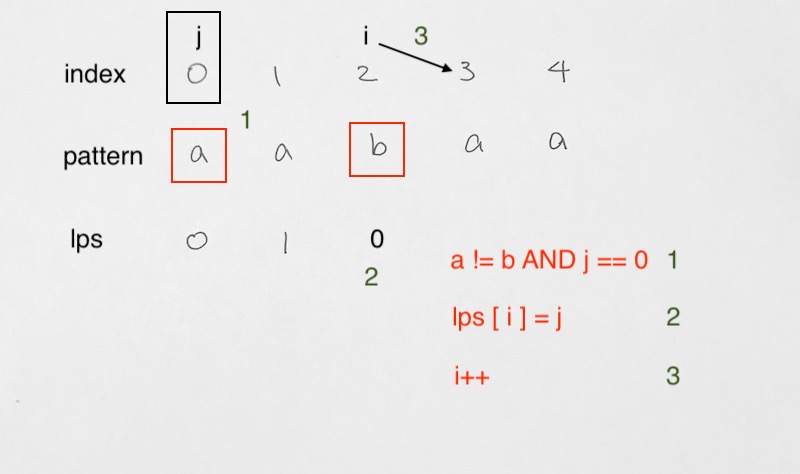
1) Match – we have a match on characters at index i and j. In this case,
1) we move j++ forward
2) and have lps[i] = j;
2) Then, i++.
The i++, j++ is to move the parallel matching forward. The lps[i] = j is so that our lps takes on the j’s index. The reason why we want our lps array to have j as values is because index j is an indicator of how many matches we currently have. i is simply the index of the substring we are checking.
2) Mismatch –
- mismatch where j != 0
- mismatch where j == 0
In this case, we assign j to lps[j-1]. Then compare values at j and i again.
Here, j has reached back to 0. There is a mismatch at i and thus, lps[i] takes on 0.
We then move i forward and start the parallel matching all over again.
We continue on in the main while loop
|
1 2 3 |
while (i < patternLength) { } |
until i has reached the end of the pattern.
Thus, the final result is:
0 1 2 3 4 (index)
a a b a a (pattern)
0 1 0 1 2 (lps)
The KMP matching algorithm
Now that we have the lps array, we can process the KMP algorithm.
First let’s set it up:
|
1 2 3 4 5 6 7 8 |
let i = 0; // index for txt[] let j = 0; // index for pat[] while (i < textLength) { if (pattern[j] == text[i]) {j++; i++;} ... ... } |
Basically, we have i as the index of text, and j as index of pattern.
If the character of text at index i matches character of pattern at index j, we simply move forward both i and j.
This way, we iterate down both arrays and compare characters in such fashion.
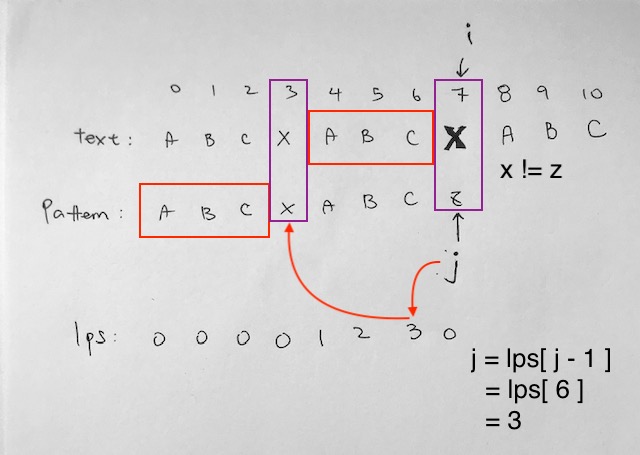
In our example, notice we move down and the characters match up like so: “a b c x a b c..” However, you should think of it as characters match taking place for prefix “abc”, then a substring “x”, then suffix “abc”. Eventually, we hit a mismatch at “x” and “z” at index 7.
A mismatch is when the characters of pattern and text are not equal, AND i is still within the text.length.
|
1 2 3 |
(i < textLength && pattern[j] != text[i]) { ... } |
Then we check to see if pattern index j is at 0 or not.
If j is at 0, it means we are at the very beginning of the pattern and cannot go backwards anymore. Thus, we simply have text index i move forward to go on with the next match.
However, if j is not 0, it means, it needs to jump back to a certain point on the pattern. The number of steps to jump back is decided by the lps array at j-1.
|
1 2 3 4 |
if (j != 0) j = lps[j - 1]; else i = i + 1; |
Now, in the standard Naive way, j comes back to index 0 (the pattern’s beginning). i goes to index 1, then they start comparing again. This is too slow and cumbersome.
The secret to KMP is that we have a Prefix Suffix array that tells us how far back j should jump on the pattern array.
The LPS array will tell j which index to jump so that we don’t have to start from the beginning of the pattern.
The LPS array will have us jump back to a certain niche between two matching substrings, the prefix and suffix.
The reason why we can jump in between the suffix and prefix substring is because on the previous match, we ran through:
prefix + substring1 + suffix
“abc” + “x” + “abc”
The suffix of the previous match (“abc”) matches our current prefix pattern (“abc”). Thus, we always start at the beginning of the substring (“x”).
Let’s continue with our example.
In our previous match, the prefix is “abc”. The substring is “x”. The suffix is “abc”.
Hence, for our next match, we don’t need to match up the prefix again. We already know that the suffix of our previous run is already a match with our current pattern’s prefix of “abc”. Hence we skip that part entirely.
Instead, j just jumps straight to the “x”. In other words, the number of steps to jump back is decided by the lps array at j-1. That is basically how the lps array helps us save steps.
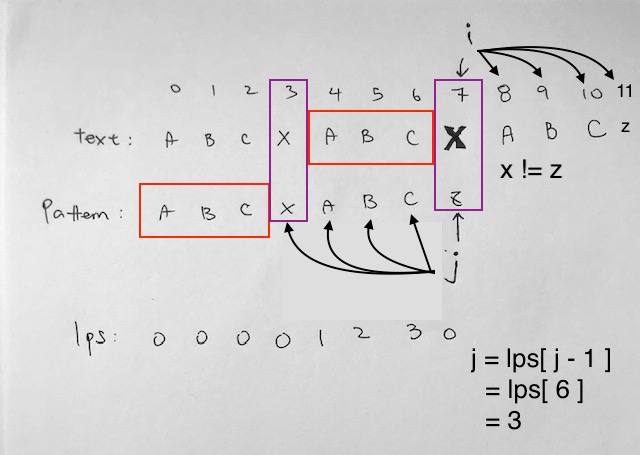
After our index j jumps to index 3, we continue matching.
text[7] = x, pattern[3] = x √
text[8] = a, pattern[4] = a √
…
…
until our index j finally runs to end of the pattern. This signifies that we have a complete pattern match.
We want to see where the index of the match happened in text, so we simply do i – j, which basically means at the last character match at index i, just subtract pattern.length in order to get the index i of where the match starts. In our case, it is i(12) – j(8) = 4.