Quick sort version
The divide and conquer recursion on an array occurs when we have dubbed a mid,
then recursively go into the left side of the array. Then, the right side. We leave the middle element.
Thus we apply recursion on
- low to (mid-1)
- print mid
- (mid+1) to high
But how?
We recursive into the left
|
1 2 |
divAndConq(arr, low, mid-1); console.log(" processing at element: " + arr[mid] + " √ "); |
1) For each step we go deeper into the leftmost array, we push one recursion onto the stack. Since we recurse first, then print, we need to push recursions on first.
2) When we reach the 0th element of the array, we have reached the leftmost (single element). Once its reached and the recursion function for the 0th element finishes, we pop it, and then continue on to the next line which is print. In other words, we then start executing the print code after the recursion.
3) When the printing is done (printing the mid), we will hit a function to process the right side.
We recursive into the right
|
1 2 |
console.log(" processing at element: " + arr[mid] + " √ "); divAndConq(arr, mid + 1, high); |
4) Due to the order of the print, and recursion, we have printed, then push a recursion function onto the stack to process the right side.
5) Once that’s done, we pop and then come back to the previous left recursion. We move on and print. Then recurse on the right side.
Let’s go into an example.
Recurse deep into the leftmost array item
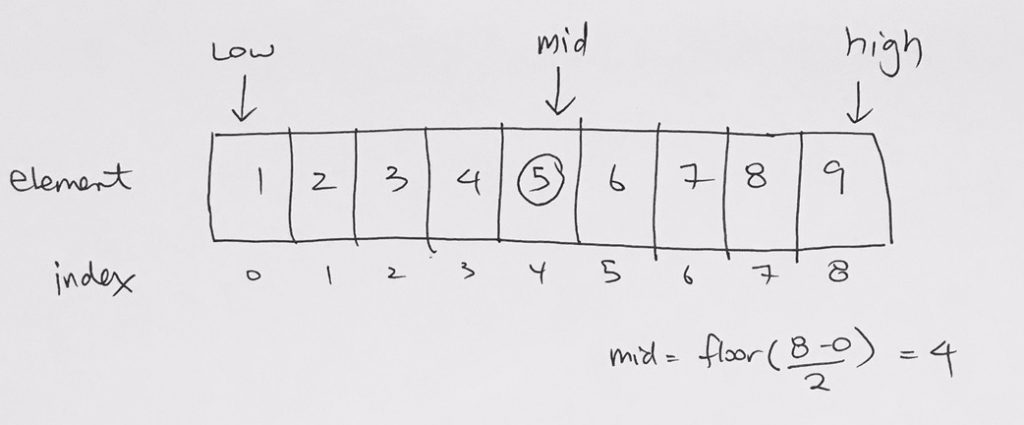
Say we have an array with 1 to 9. Indexed from 0 to 8. The concept of recursive divide and conquer is that we calculate a pivot first. The pivot is calculated to be somewhere in the middle of the array, then the left and right array are recursively processed.
For simplification purposes, we want to keep things simple. So let’s calculate the pivot such that it is:
floor of (low + high)/2
low: 0
high: 8
pivot = floor(4) = 4, we’ll print this pivot AFTER we process the left array
Our pivot will be printed after all the left array is processed.
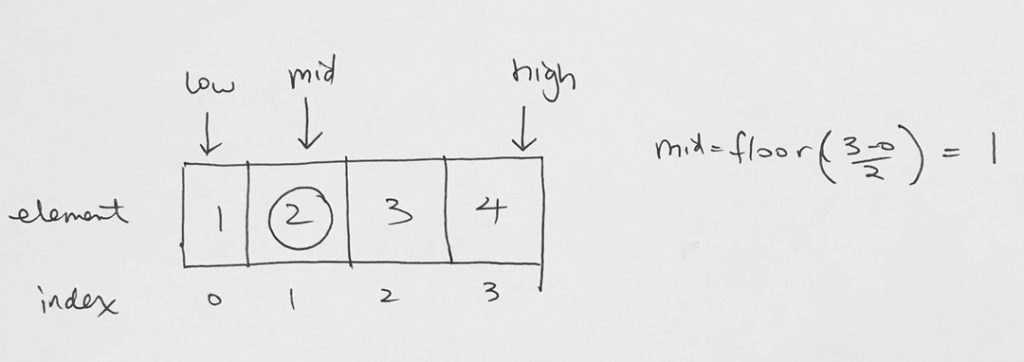
Then we recursively process the left array.
low: 0
high: 3
pivot = floor( 0 + 3 /2 ) = 1, we’ll print this pivot AFTER we process the left array
left array is divAndCon(0, 1-1) or divAndCon(0,0)
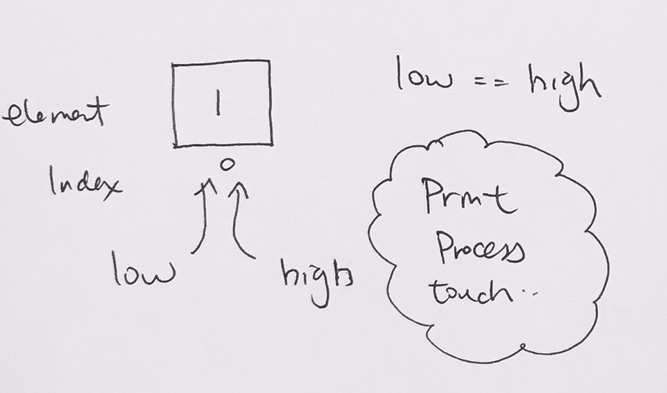
It happens that divAndCon(0, 0) is a base case (We notice that low == high) and thus, simply prints 0. We then pop the current recursion function and move on.
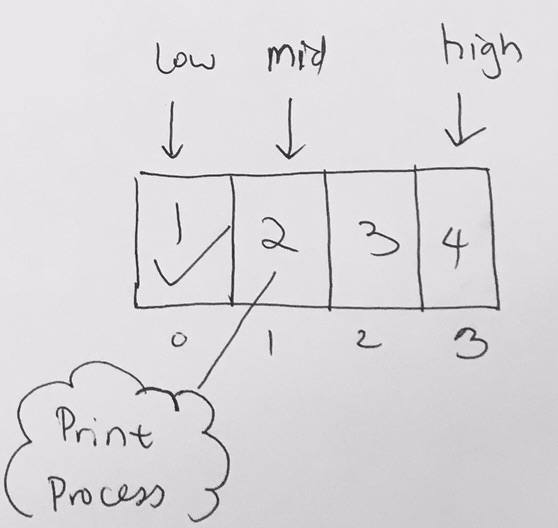
Processing the right array
Now we pop back to the previous recursion with indexes divAndCon(0, 3). Since we’ve processed the left array of [1], we need to print the mid, which is index 1, element 2. Then we move on to process the right array [2,3]
right array is divAndConq(2,3)
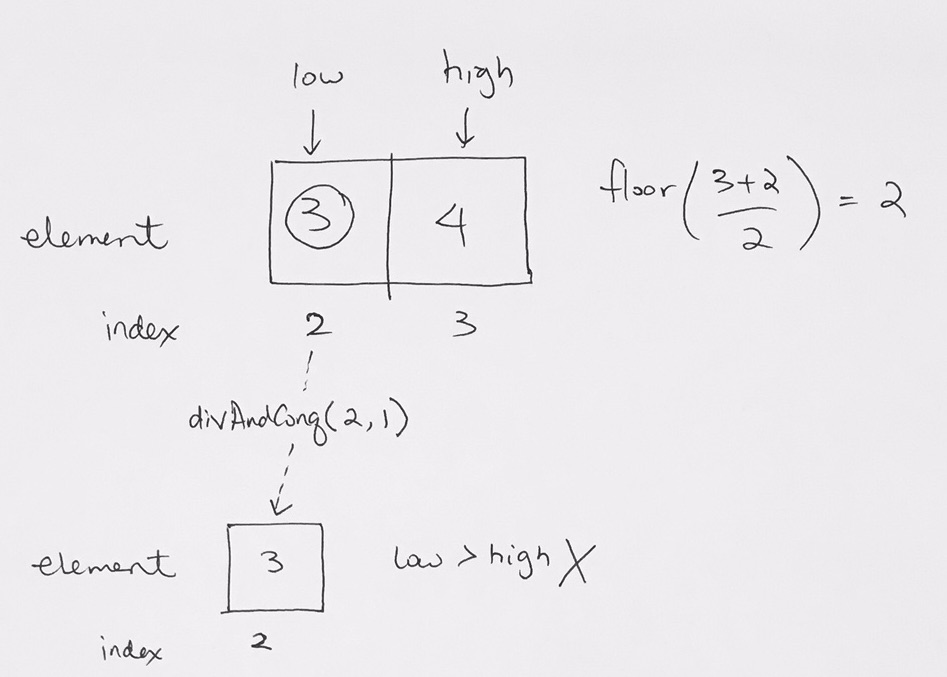
Notice the array we’re processing is [3,4] where:
low: 2
high: 3
mid = floor of (3 + 2 ) / 2 = 2, we’ll print this pivot AFTER we process the left array
left array is divAndCon(2, 2-1) or divAndCon(2, 1)
When we reach to divAndConq(2,1) we see that low > high is false. Thus, we don’t do anything and just return
Once we return, we need to print the the pivot, which is element 3 at index 2.
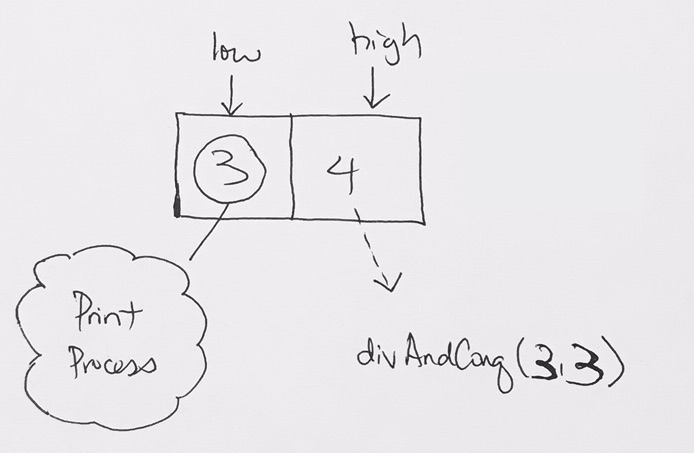
Then process the right array, which is divAndCon(2+1,3), divAndConq(3,3)
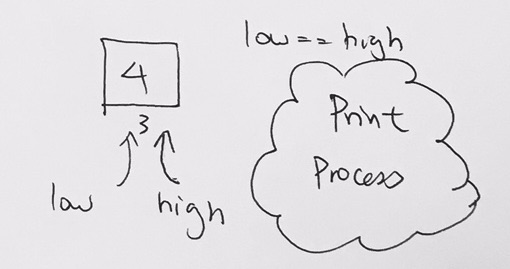
divAndConq(3,3), we see that low == high, and we print (process)
So as you can see, this is how each element is printed (processed) from the beginning to end in a recursive fashion on an array.
Left Recursion not available
There comes a situation where the start index is larger than the end index…
for example, say we’re at recursion where index is 2 and 3.
[2:X][3:Y]
midpoint = (3 – 2)/2 = 0.
So we go into the LEFT recursion like so divideAndConquer(0, 0-1), or divideAndConquer(0,-1).
Under such case, we do not have a left section to go into. We already have mid pointing to the first element in the current array at [2:X].
Thus, mid will print, and all we have to do is take care of the right element [3:Y] in our right recursion.
Hence, we have to implement a base case to avoid this situation:
whenever start > end, we simply return
Source Code
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
var arr = [1,2,3,4,5,6,7,8,9]; function partition(arr, low, high) { return Math.floor((low + high) / 2); } function divAndConq(arr, low, high) { console.log("\ndivAndConq: [" + low + ", " + high + "]"); if (low == high) { console.log(" processing at element: " + arr[low] + " √ "); return; } if (low < high) { var mid = partition(arr, low, high); console.log(low + " < " + high + "? √, " + "middle is: " + mid); divAndConq(arr, low, mid-1); console.log(" processing at element: " + arr[mid] + " √ "); divAndConq(arr, mid + 1, high); } else { // low > high skips console.log(low + " > " + high + "? X"); } } divAndConq(arr, 0, arr.length-1); |
output
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
divAndConq: [0, 8] 0 < 8? √, middle is: 4 divAndConq: [0, 3] 0 < 3? √, middle is: 1 divAndConq: [0, 0] processing at element: 1 √ 0 < 0? X processing at element: 2 √ divAndConq: [2, 3] 2 < 3? √, middle is: 2 divAndConq: [2, 1] 2 < 1? X processing at element: 3 √ divAndConq: [3, 3] processing at element: 4 √ 3 < 3? X processing at element: 5 √ divAndConq: [5, 8] 5 < 8? √, middle is: 6 divAndConq: [5, 5] processing at element: 6 √ 5 < 5? X processing at element: 7 √ divAndConq: [7, 8] 7 < 8? √, middle is: 7 divAndConq: [7, 6] 7 < 6? X processing at element: 8 √ divAndConq: [8, 8] processing at element: 9 √ 8 < 8? X |
Using divide and conquer to loop
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
var arr = [1,2,3,4,5,6,7,8,9]; function partition(arr, low, high) { return Math.floor((low + high) / 2); } function divAndConq(arr, low, high, callback) { if (low == high ) { arr[low] = callback(arr[low], low); } if (low > high) { console.log("Ignore previous element. Stay in our lane"); } if (low < high) { var pi = partition(arr, low, high); divAndConq(arr, low, pi-1, callback); arr[pi] = callback(arr[pi], pi); divAndConq(arr, pi + 1, high, callback); } } console.log(arr); divAndConq(arr, 0, arr.length-1, function(element, index) { console.log("element: " + element + ", index: " + index); return element * 2; }); console.log(arr); |
output
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
[ 1, 2, 3, 4, 5, 6, 7, 8, 9 ] element: 1, index: 0 element: 2, index: 1 Ignore previous element. Stay in our lane element: 3, index: 2 element: 4, index: 3 element: 5, index: 4 element: 6, index: 5 element: 7, index: 6 Ignore previous element. Stay in our lane element: 8, index: 7 element: 9, index: 8 [ 2, 4, 6, 8, 10, 12, 14, 16, 18 ] |
MergeSort version
The difference is that the recursion in mergesort does not leave out the mid element. It includes the mid element as part of the right array. Thus, that’s why we use Math.ceil when we divide the array. Thus the recursion is applied on
- low to (mid – 1)
- mid to high
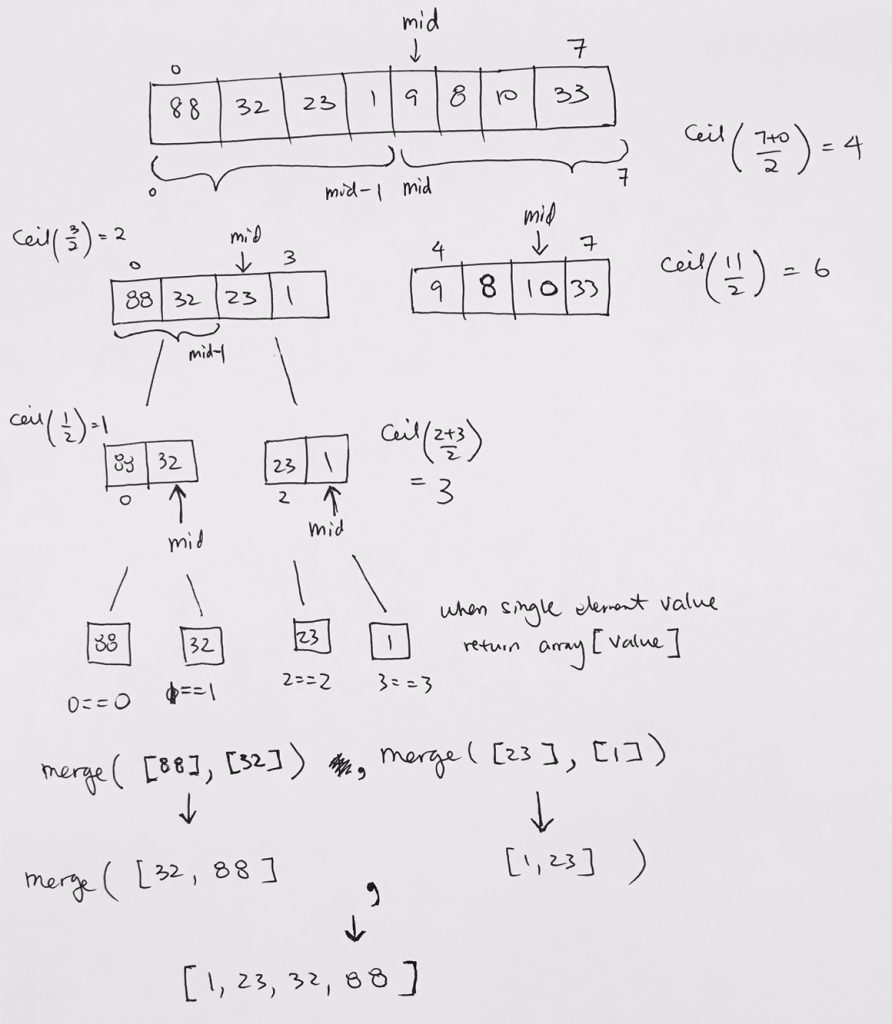
We want to drill down to the single element itself, which is when low == high. Then we simply return it. The merge function then proceeds to calculate and sort the returned single elements in 2s. Sorting first, 2 elements. Then the next merge call will sort 4 elements. Then sort 8 sorts, and so on.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
var arr = [88, 32, 23, 1,9,8, 10, 33, 56, 65, 35, 52, 15, 78, 98, 89, 100, 2,3,11,22,31,44,56,66]; function partition(arr, low, high) { return Math.ceil((low + high) / 2); } function divAndConq(arr, low, high) { console.log("\ndivAndConq: [" + low + ", " + high + "]"); if (low == high) { console.log(" processing at element: " + arr[low] + " √ "); return [arr[low]]; } if (low < high) { // low >= high skips var mid = partition(arr, low, high); console.log("mid: " +mid); return merge( divAndConq(arr, low, mid-1), divAndConq(arr, mid, high) ); } } divAndConq(arr, 0, arr.length-1); |
where the merge happens like so:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
function merge(leftArr, rightArr) { if (leftArr.length < rightArr.length) { smallerArray = leftArr; biggerArray = rightArr; } else { smallerArray = rightArr; biggerArray = leftArr; } var smallIndex = 0, largeIndex = 0; // Merge sort requires a temporary array to merge the sorted arrays and hence it is not in-place // this result arr is the temporary array, which requires more space. var result = []; while (smallerArray[smallIndex] && biggerArray[largeIndex]) { var nextSmallerItem = (smallerArray[smallIndex] < biggerArray[largeIndex]) ? smallerArray[smallIndex++] : biggerArray[largeIndex++]; result.push(nextSmallerItem); } return (smallerArray[smallIndex]) ? result.concat(smallerArray.splice(smallIndex)) : result.concat(biggerArray.splice(largeIndex)); } |
output
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 |
divAndConq: [0, 24] mid: 12 divAndConq: [0, 11] mid: 6 divAndConq: [0, 5] mid: 3 divAndConq: [0, 2] mid: 1 divAndConq: [0, 0] processing at element: 88 √ divAndConq: [1, 2] mid: 2 divAndConq: [1, 1] processing at element: 32 √ divAndConq: [2, 2] processing at element: 23 √ divAndConq: [3, 5] mid: 4 divAndConq: [3, 3] processing at element: 1 √ divAndConq: [4, 5] mid: 5 divAndConq: [4, 4] processing at element: 9 √ divAndConq: [5, 5] processing at element: 8 √ divAndConq: [6, 11] mid: 9 divAndConq: [6, 8] mid: 7 divAndConq: [6, 6] processing at element: 10 √ divAndConq: [7, 8] mid: 8 divAndConq: [7, 7] processing at element: 33 √ divAndConq: [8, 8] processing at element: 56 √ divAndConq: [9, 11] mid: 10 divAndConq: [9, 9] processing at element: 65 √ divAndConq: [10, 11] mid: 11 divAndConq: [10, 10] processing at element: 35 √ divAndConq: [11, 11] processing at element: 52 √ divAndConq: [12, 24] mid: 18 divAndConq: [12, 17] mid: 15 divAndConq: [12, 14] mid: 13 divAndConq: [12, 12] processing at element: 15 √ divAndConq: [13, 14] mid: 14 divAndConq: [13, 13] processing at element: 78 √ divAndConq: [14, 14] processing at element: 98 √ divAndConq: [15, 17] mid: 16 divAndConq: [15, 15] processing at element: 89 √ divAndConq: [16, 17] mid: 17 divAndConq: [16, 16] processing at element: 100 √ divAndConq: [17, 17] processing at element: 2 √ divAndConq: [18, 24] mid: 21 divAndConq: [18, 20] mid: 19 divAndConq: [18, 18] processing at element: 3 √ divAndConq: [19, 20] mid: 20 divAndConq: [19, 19] processing at element: 11 √ divAndConq: [20, 20] processing at element: 22 √ divAndConq: [21, 24] mid: 23 divAndConq: [21, 22] mid: 22 divAndConq: [21, 21] processing at element: 31 √ divAndConq: [22, 22] processing at element: 44 √ divAndConq: [23, 24] mid: 24 divAndConq: [23, 23] processing at element: 56 √ divAndConq: [24, 24] processing at element: 66 √ |
Futher study
If you want to reverse the display of the array, simply reverse your recursion like so:
|
1 2 |
divAndConq(arr, mid, high); divAndConq(arr, low, mid-1); |
This way, you look at the high end first, which is the upper half. Then the next recursion will go upper half. so on, and so on, until you hit the last element first.