http://www.geeksforgeeks.org/insertion-sort/

Insertion sort is a simple sorting algorithm that works the way we sort playing cards in our hands
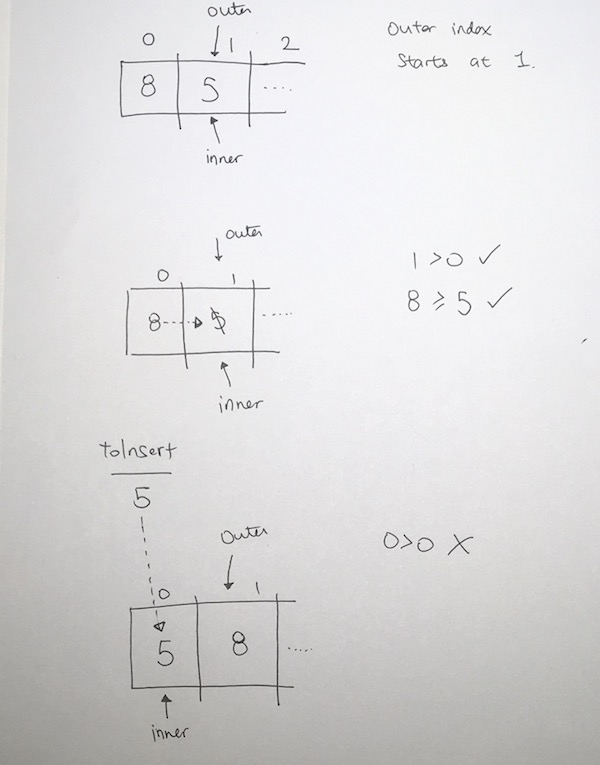
Say we’re given a data set, 8 5 3 12 2
Option 1 – previous is larger
We start off the algorithm at index 1.
So we see 5 and store it in a temp variable.
There are 2 conditions we must satisfy:
1) Is the current index > 0 ? (1 > 0 ? yes )
2) Is the previous element is larger than our temp? 8 > 5, yes.
Both satisfies so we copy the previous element (8) to the current location where 5 is.
We move 1 step back and hit index 0.
We evaluate the 2 situations again:
1) 0 > 0, no. We stop.
If we reach index 0, that means we’ve reached the end, and we store 5 there.
We then move on to index 2 and continue processing in the same manner.
Option 2 – previous is smaller
If say we have 3 5 7.
We start off at index 1.
We see 5 and store it in a temp variable.
There are 2 conditions we must satisfy:
1) Is the current index > 0 ? (1 > 0 ? yes )
2) Is the previous element is larger than our temp? 3 > 5, no.
In this case, we don’t do anything move onto the next index 2.
This is the part where if the whole array is sorted, we only execute this comparison and then move on to the next index. Since the previous will always be smaller than the current, we simply stop and move on. Hence, the best case is O(n) because we do execute a comparison at every index once. We do this for every element and then stop.
Insertion sort takes the current number and go backwards to see where to insert it. We do this by comparing the previous element and seeing if its bigger than our valueToInsert. If it’s larger, push it down and we keep going. If it’s smaller, we stop and we insert our number. If we reach the end at index 0, we insert our number.
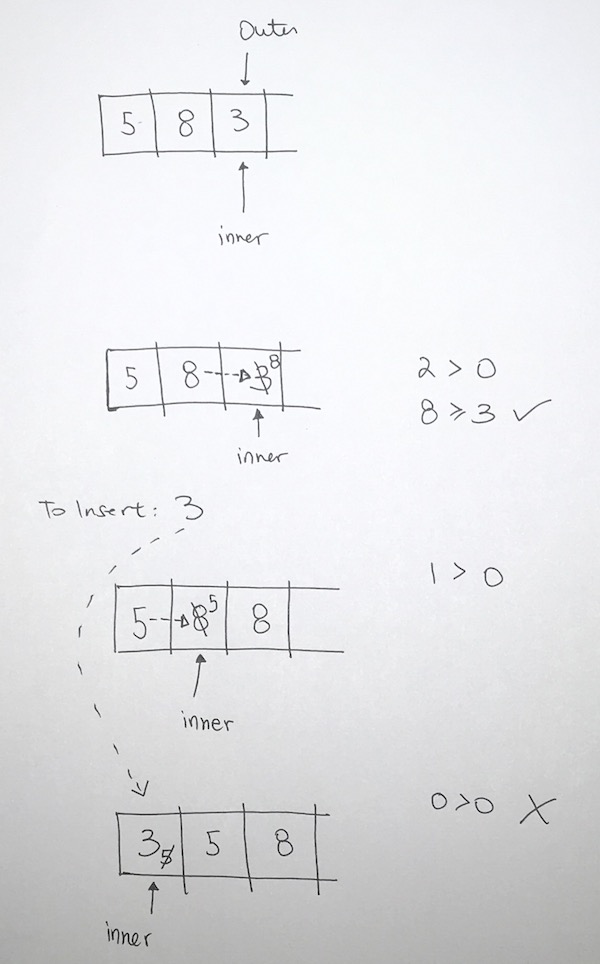
Now we have 5 8 3 12 2.
We work our next pass which is index 2 with value 3.
We store 3 and start searching for the insertion point. We evaluate the 2 points:
1) is index > 0? 2 > 0, yes.
2) We look at the previous element 8. is 8 > 3? yes, so we move 8 to where 3 is.
Move backwards 1 step.
1) is index > 0? 1 > 0, yes.
2) Then we look at previous element 5, is 5 > 3? yes. so we move 5 to where 8 is.
1) is index > 0? 0 > 0, no. We’ve reached the end. Hence we put 3 at index 0.
This leaves us with 3 5 8 12 2.
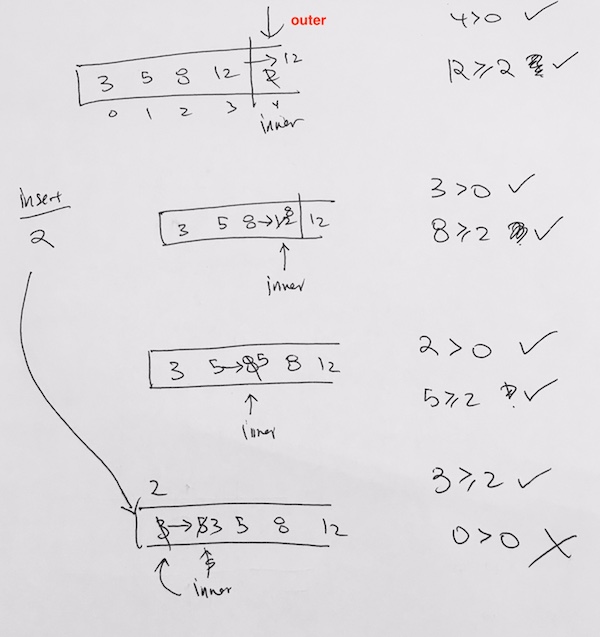
Then we work on value 12.
1) is index > 0? index 3 > 0, yes.
2) Previous element 8 > 12?
no. We stop, and move on.
Moving on…finally, our last value is 2. Apply the same as we did above and we’ll see that 2 will be inserted at the way in the beginning because it is smaller than the other numbers.

Time Complexity
The best case input is an array that is already sorted. In this case insertion sort has a linear running time (i.e., O(n)). During each iteration, the first remaining element of the input is only compared with the right-most element of the sorted subsection of the array.
The simplest worst case input is an array sorted in reverse order. The set of all worst case inputs consists of all arrays where each element is the smallest or second-smallest of the elements before it. In these cases every iteration of the inner loop will scan and shift the entire sorted subsection of the array before inserting the next element. This gives insertion sort a quadratic running time O(n^2).
The average case is also quadratic, which makes insertion sort impractical for sorting large arrays.
However, insertion sort is one of the fastest algorithms for sorting very small arrays, even faster than quicksort; indeed, good quicksort implementations use insertion sort for arrays smaller than a certain threshold, also when arising as subproblems; the exact threshold must be determined experimentally and depends on the machine, but is commonly around ten.