Hash Map (chaining) | Chinese Rule of Eight

demo

ref –
http://www.algolist.net/Data_structures/Hash_table/Chaining
http://stackoverflow.com/questions/9214353/hash-table-runtime-complexity-insert-search-and-delete

Hash Map with Chaining

The load factor is a measure of how full the hash table is allowed to get before its capacity is automatically increased.

When the number of entries in the hash table exceeds the product of the load factor and the current capacity,
the hash table is rehashed (that is, internal data structures are rebuilt) so that the hash table has
approximately twice the number of buckets.

The Node

.h file

#include <stdio.h>

class LinkedHashEntry {

public:

//life cycle

LinkedHashEntry(int key, int value);

~LinkedHashEntry();

// get set methods

void setKey (int newKey);

void setValue (int newValue);

void setNext (LinkedHashEntry * newNext);

int getKey();

int getValue();

LinkedHashEntry * getNext();

private:

LinkedHashEntry * next;

int key;

int value;

};

.cpp file

#include "LinkedHashEntry.hpp"

LinkedHashEntry::LinkedHashEntry(int key, int value) {

this->key = key;

this->value = value;

this->next = NULL;

}

LinkedHashEntry::~LinkedHashEntry() {

this->key = -1;

this->value = -1;

this->next = NULL;

}

void LinkedHashEntry::setKey(int newKey) {

this->key = newKey;

}

void LinkedHashEntry::setValue(int newValue) {

this->value = newValue;

}

void LinkedHashEntry::setNext(LinkedHashEntry * newNext) {

this->next = newNext;

}

int LinkedHashEntry::getKey() {

return this->key;

}

int LinkedHashEntry::getValue() {

return this->value;

}

LinkedHashEntry * LinkedHashEntry::getNext() {

return this->next;

}

The Hash Map

#include <stdio.h>

#include <iostream>

#include "LinkedHashEntry.hpp"

const int TABLE_SIZE = 8;

class HashTable {

public:

//remove element by key

void remove(int key);

// put the key and value into the table.

// if key already exist, replace value

void put(int key, int value);

void print();

// remove value by key

HashTable();

~HashTable();

private:

// array of pointers

// table points to the address of 1st pointer in the array

LinkedHashEntry ** table;

};

HashTable.hpp

The way we go about creating the Hash Table is by using an array of pointers. Each pointer at array[i] will point to a node. That node can link to another node. This is so that we can have an array of linked list. Which by definition, is what constitutes a chained hash map.

Thus, we use double pointers to point to this array of pointers: LinkedHashEntry ** table.

*table (or table[0]) dereferences the 1st array element.
*(table+1) (or table[1]) dereferences the 2nd array element.
..and so on

In order to allocate memory, we allocate this array of pointers on the heap.

Think of it like this:

We want to allocate on the heap (new)
an array of certain size ([MAX])
of LinkedHashEntry pointers (LinkedHashEntry *):

LinkedHashEntry ** table = new LinkedHashEntry * [MAX]

By definition, we always have a pointer pointing to the address of the first element of the array.

In every array, we always assign an array anchor (a pointer) to the 1st element of the array.
For example, an array of integers, int * i = new int [8];

int * i points to the first integer element’s address.
*i will dereference and get the int value.

In our case, since our first element is a pointer, we need a pointer to a pointer to act as the array anchor, and that is
why we use LinkedHashEntry ** table.

Now, we have an array of LinkedHashEntry pointers, and we are set to work.

#include "HashTable.hpp"

#include "LinkedHashEntry.hpp"

#pragma mark - life cycle

HashTable::HashTable() {

//1) allocate an array of LinkedHashEntry pointers

this->table = new LinkedHashEntry * [TABLE_SIZE];

//2) initialize all the pointers to NULL

for ( int i = 0; i < TABLE_SIZE; i++) {

//pointer

this->table[i] = NULL;

}

HashTable::~HashTable() {

std::cout << "\n\n\n~~~DEALLOCATION PROCESS STARTED ~~~" << std::endl;

for ( int i = 0 ; i < TABLE_SIZE; i++) {

std::cout << "----Deallocating for slot[" << i << "]----" << std::endl;

if(this->table[i] != NULL) {

LinkedHashEntry ** temp = &this->table[i];

while(*temp != NULL) {

LinkedHashEntry * toDelete = *temp;

*temp = (*temp)->getNext();

deleteNode(toDelete);

}

} else {

std::cout << "\n array element pointing to NULL" << std::endl;

}

delete this->table;

std::cout << "~~~DEALLOCATION COMPLETE ~~~\n\n\n" << std::endl;

}

#pragma mark - instance methods

void HashTable::print() {

std::cout << "------ PRINTING RESULTS -----" << std::endl;

for ( int i = 0; i < TABLE_SIZE; i++) {

std::cout << "--------[" << i << "]-----------" << std::endl;

if (this->table[i] != NULL) {

//traverse

for (LinkedHashEntry * temp = this->table[i]; temp != NULL; temp = temp->getNext()) {

//display all data

std::cout << "\nkey: " << temp->getKey()

<< ", value: " << temp->getValue()

<< std::endl;

}

} else {

std::cout << " THIS SLOT IS EMPTY" << std::endl;

}

} //for

std::cout << "=====================\n\n\n" << std::endl;

}

Insertion

While certain operations for a given algorithm may have a significant cost in resources, other operations may not be as costly.

Amortized analysis considers both the costly and less costly operations together over the whole series of operations of the algorithm. This may include accounting for different types of input, length of the input, and other factors that affect its performance

insertion O(1) average and amortized case complexity, however it suffers from O(n) worst case time complexity.

BUT WHY?
Hash tables suffer from O(n) worst time complexity due to two reasons:

If too many elements were hashed into the same key. Thus, it degrades into a linked list
for that particular slot. Searching through this list may take O(n) time. see 2), where it keeps appending elements at the same slot.

Once a hash table has passed its load balance, it has to rehash [create a new bigger table, and re-insert each element to the table].

The reason why it is O(1) average and amortized case because:

It is very rare that many items will be hashed to the same key
if you chose a good hash function and you don’t have too big load balance.
The rehash operation, which is O(n), can at most happen after n/2 ops
which are all assumed O(1): Thus when you sum the average time per op, you get : (n*O(1) + O(n)) / n) = O(1)

void HashTable::put(int key, int value) {

int index = key % TABLE_SIZE;

if(this->table[index]==NULL) {

std::cout << "[" << index << "] is empty. Append initial Entry." << std::endl;

this->table[index] = new LinkedHashEntry(key, value);

} else { //there exist element at this slot

//if there already exist...let's traverse and look if that key exist

LinkedHashEntry * traverser = this->table[index];

LinkedHashEntry * last = traverser;

while(traverser != NULL) {

//1) if found the key that matches, let's simply replace value

if (traverser->getKey() == key) {

std::cout << "A similar key is found at [" << index << "], we replace it with value " << value << std::endl;

traverser->setValue(value);

return; //done!

} else { //go down

last = traverser;

traverser = traverser->getNext();

}

// 2) no same key found, this is a new key, append!

std::cout << " this is a unique key, simply append to " << "[" << index << "]" << std::endl;

last->setNext(new LinkedHashEntry(key, value));

}

Deletion

Deletion has the same concept as Insertion. Amortized case O(1), worst time O(n).

deleteNode is just a simple function that sets a LinkedHashEntry pointer to NULL and wipes out everything.

void deleteNode(LinkedHashEntry * toDelete) {

std::cout << "\n====================" << std::endl;

std::cout << "Deleting node with key: " << toDelete->getKey() << std::endl;

std::cout << "value: " << toDelete->getValue() << std::endl;

std::cout << "====================\n" << std::endl;;

toDelete->setKey(-1);

toDelete->setValue(-1);

delete toDelete;

toDelete = NULL;

}

recurseAndRemove uses recursion to run through a list of LinkedHashEntry nodes, and remove the node with the specified key.

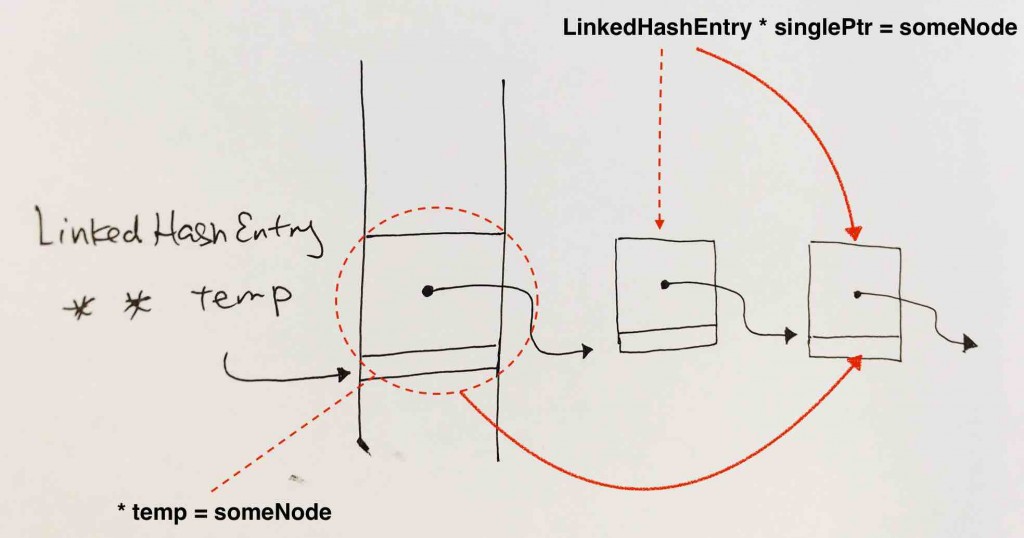
The list of nodes is given by LinkedHashEntry ** temp. Pointer of a pointer means that the double pointer points to the the address of a pointer. That pointer points to the address of the node.

Hence, if we want to reassign the pointer at this->table[i] to another node, it means:

this->table[i] is a pointer, thus we have to use a double pointer (HashEntry ** temp) to point to this->table[i]. Deference it like this (*temp) to control the pointer this->table[i] itself….and assign it to another node as shown in the image.

If we simply have a pointer like HashEntry * singlePtr = this->table[i], it won’t work because singlePtr will be pointing to whatever this->table[i] is pointing to. singlePtr is pushed onto the local stack, and has nothing to do with the pointer that is this->table[i].

singlePtr simply points to whatever this->table[i] points to. singlePtr is pushed onto the local stack

Once you understand this, the rest is just simple recursion and node traversal.

There are 2 cases:

You need to remove the first node. This means in order to get control of the first pointer, you need to get the address of the initial pointer, dereference it (at this point, you have full control of the pointer) and point it
You need to remove 2nd..and after node. This is simple because dereferencing the temp pointer gives you full control of the next pointer.

void recurseAndRemove(LinkedHashEntry ** temp, LinkedHashEntry * previous, int key) {

std::cout << "currently evaluating node with key: " << (*temp)->getKey()

<< ", and value: " << (*temp)->getValue();

if((*temp)->getKey()==key) {

std::cout << "\n  Found key " << key << std::endl;

LinkedHashEntry * toErase = *temp;

//1) removing 1st node

if(*temp == previous) {

*temp = previous->getNext();

} else {

//2) removing 2nd and after node

previous->setNext((*temp)->getNext());

}

deleteNode(toErase);

return; //done

}

LinkedHashEntry * next = (*temp)->getNext();

std::cout << "\nNext key to evaluate is: " << next->getKey()

<< ", value: " << next->getValue() << std::endl;

recurseAndRemove( &next,

*temp,

key);

}

void traverseAndRemove(LinkedHashEntry ** initialSlotPtr, int key) {

LinkedHashEntry * listTraversal = *initialSlotPtr;

LinkedHashEntry * follower = *initialSlotPtr;

while(listTraversal != NULL) {

if(listTraversal->getKey() == key) {

std::cout << "Found matching key " << key << ", with value " << listTraversal->getValue() << std::endl;

std::cout << "Let's remove this!" << std::endl;

if(listTraversal == follower) { // single node

*initialSlotPtr = listTraversal->getNext();

} else { // multiple node

follower->setNext(listTraversal->getNext());

}

deleteNode(listTraversal);

return;

} else {

follower = listTraversal;

listTraversal = listTraversal->getNext();

}

} // while

}

void HashTable::remove(int key) {

std::cout << "Let's remove the node with key:" << key << std::endl;

int index = key % TABLE_SIZE;

//we have to find

if(this->table[index] == NULL) {

std::cout << "Not value exist for this Key" << std::endl;

return;

} else {

//traverseAndRemove(&this->table[index], key);

recurseAndRemove(&this->table[index],

this->table[index],

key);

} // else

}