ref – https://github.com/redmacdev1988/LinearProbeHashTable
https://stackoverflow.com/questions/9124331/meaning-of-open-hashing-and-closed-hashing
Linear Probing is an Open Addressing scheme for hash tables.
The “open” in “open addressing” tells us the index (aka. address) at which an object will be stored in the hash table is not completely determined by its hash code. Instead, the index may vary depending on what’s already in the hash table.
The “closed” in “closed hashing” refers to the fact that we never leave the hash table; every object is stored directly at an index in the hash table’s internal array. Note that this is only possible by using some sort of open addressing strategy. This explains why “closed hashing” and “open addressing” are synonyms.
Best case – O(1).
For insertion, it hashes to an empty element. We insert. done.
For search, it hashes to its initial location. We do a check. Keys match. done.
Deletion – Searches for the element with the key. We find it. We remove it. The next element is empty so we’re done.
Worst case – all are O(n), because the worst possible case scenario is that we have to iterate the whole array after the initial collision.
Insertion
Insertion for linear probe deals with 2 steps:
1) hash to a location. If the location is empty, done.
2) If the location is occupied, we probe for an empty space.
Probe involves going step by step down the cells and trying to find an empty cell. Once found, we place the object there.
Note that we do not circle around back to the beginning of the array. If no empty cells are to be found, we return -1. Other alternatives can be to grow the array and try inserting again.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
function probeAndInsert(kvPair, startingIndex, lastIndex) { if (startingIndex >= lastIndex) {return -1;} for (let i = startingIndex; i < lastIndex; i++) { if (!_self.array[i]) { _self.array[i] = kvPair; return i; } } console.log(`probe - uh oh, cannot find location for ${kvPair}`); return -1; } function insert(kvPair) { if (kvPair.constructor.name === "KVPair") { let index = hash(kvPair.key); kvPair.hash = index; if (!_self.array[index]) {_self.array[index] = kvPair;} else { let indexInserted = probeAndInsert(kvPair, index, _self.array.length); if (indexInserted !== -1) console.log(`insert - collision happened at ${index}... probed and inserted (${kvPair.key}) at ${indexInserted}`); else {console.log(`insert - !!! can't find a valid spot for ${kvPair.key}:${kvPair.value}`);return -1;} } } // if KVPair } |
Retrieving the object
Searching for a cell with a certain key involves starting at the hashed index:
1) If the keys match, then return the cell. If no match, keep going forward (probe) and looking for a match on our key.
2) If an empty cell is found, the key is not in the table. If the key did exist, it would be placed in the empty cell first, and not have gone any further in the later cells. This is because during insertion, when a value is hashed and there is a collision, it would naturally probe until it finds an empty spot to put its object. Thus, when searching, hitting an empty spot means its the end of the line for a particular item that was hashed to a previous location.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
// takes in a key, returns KVPair object this.retrieveIndex = function(key) { let index = hash(key); console.log(`retrieve - initially hashed ${key} to index ${index}`) // beginning with the cell at index h(x) for (let i = index; i < this.array.length; i++) { let item = this.array[i]; // if an empty cell is found, the key cannot be in the table, // because it would have been placed in that cell in preference // to any later cell that has not yet been searched. // In this case, the search returns as its result that the key // is not present in the dictionary if (!item) { console.log(`index ${i} is empty. ${key} not found`); return null; } if (item && (item.key === key)) { // If a cell containing the key is found, // the search returns the value from that cell return i; } } } |
Deleting an Object
Deleting an item is the same as searching. When we have successfully found the cell it delete, we:
1) remove the cell so the array element references null
2) Here’s the important part. Once the element was is removed in 1), we need to find a replacement down the line. The reason why we need to find a replacement is shown below.
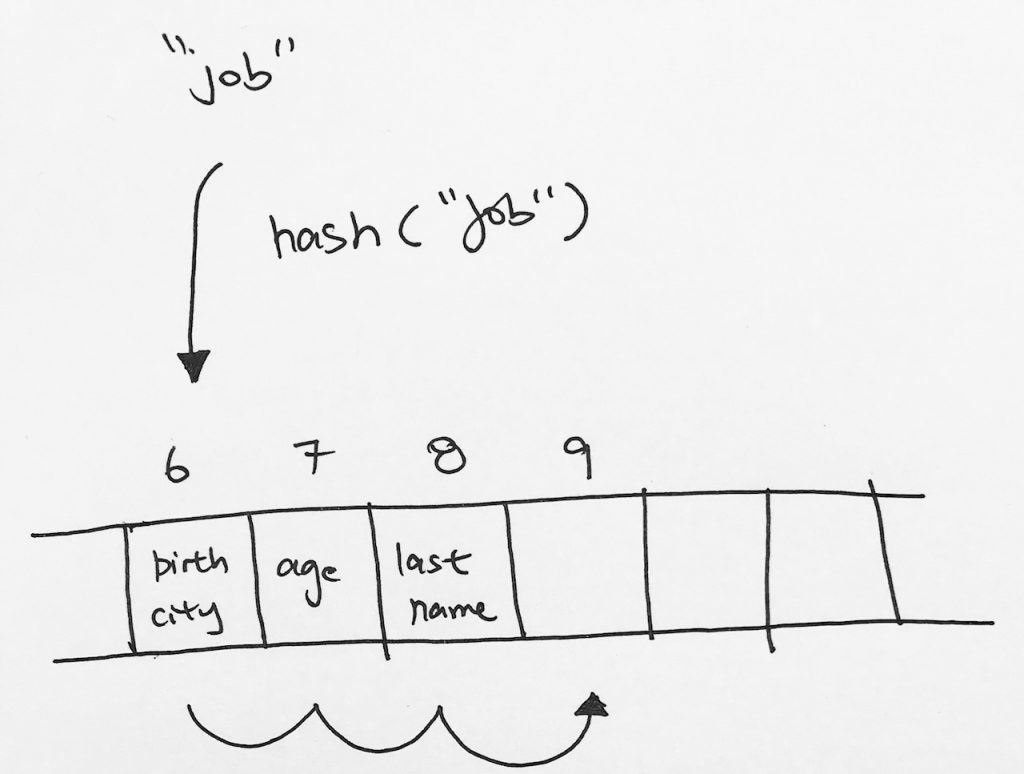
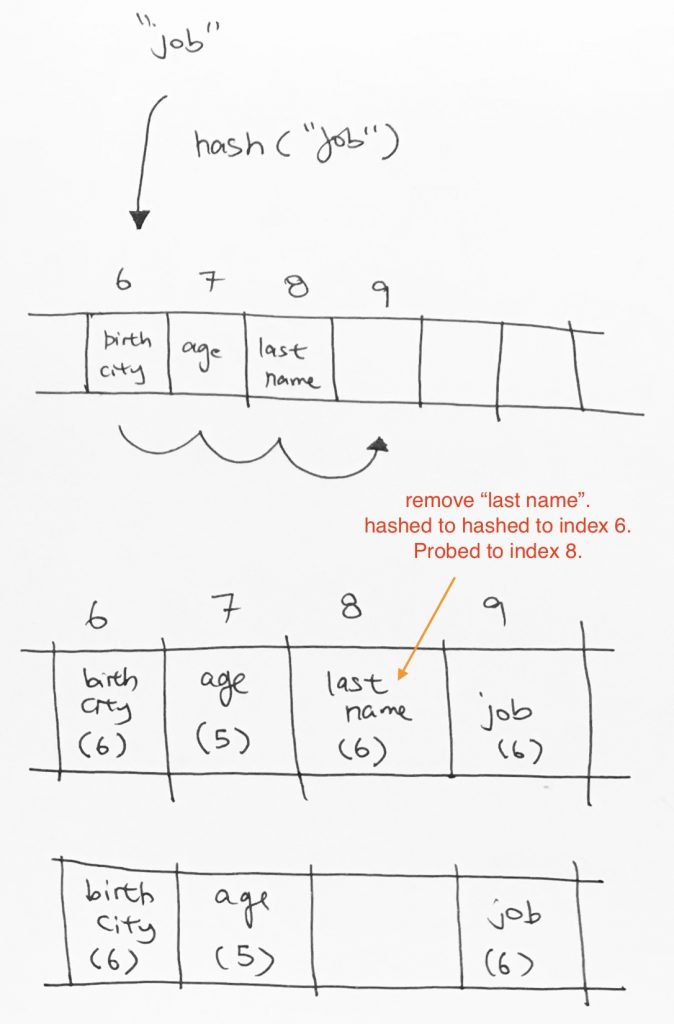
Say we want to insert key “job”. It gets hashed to index 6, then we move it to the next empty space, which is index 9.
The next operation is that we want to remove key “last name”. So last name gets hashed to index 6. We go down the array until we find “last name” at index 8. We remove it.
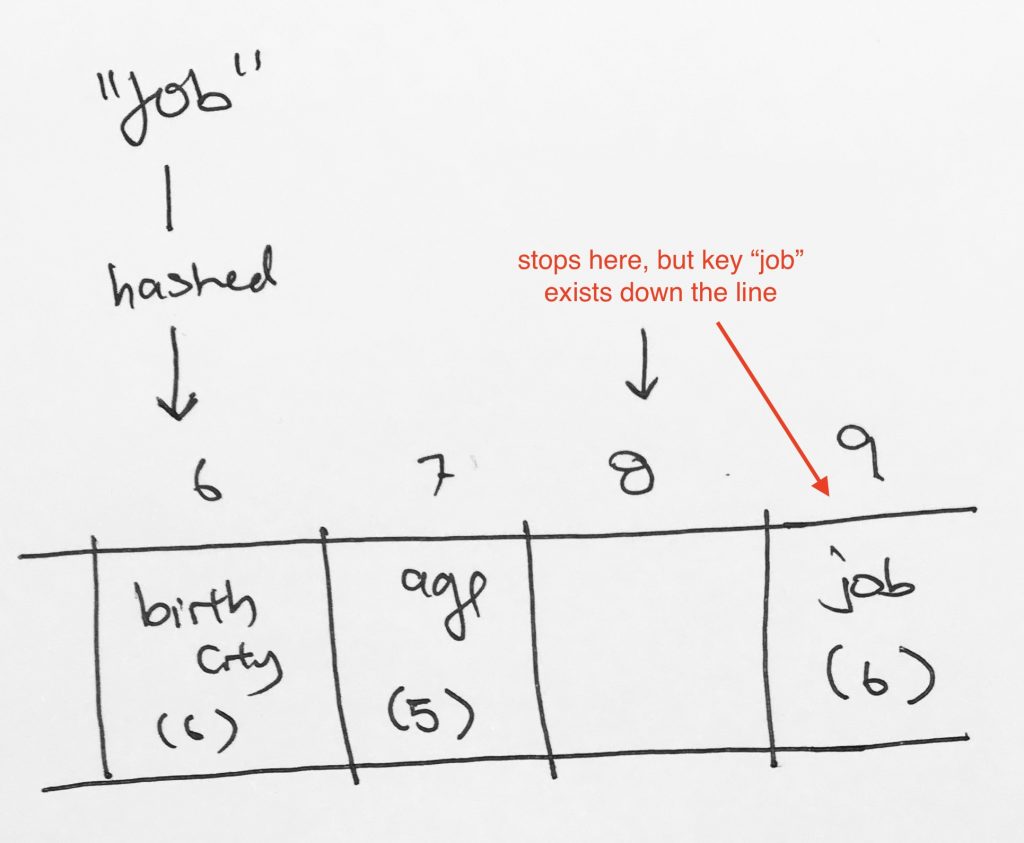
Now, say we want to search for key “job”. It would get hashed to index 6. Then it would keep going and then it would hit index 8 on an empty cell. It would stop and say key “job” does not exist. However, clearly, job exists down the line at index 9.
Solution on what to do for the empty space after deletion
When deleting, we remove the cell, then:
1) then go down the list to find a replacement for this empty cell
2) The replacement must have a key equal or smaller than the recently deleted item.
This is because all items are inserted on or after its initial hashed index. Thus, we can replace the empty cell with hashed index that is smaller because the search is coming from the left.
But why? take a look at an example:
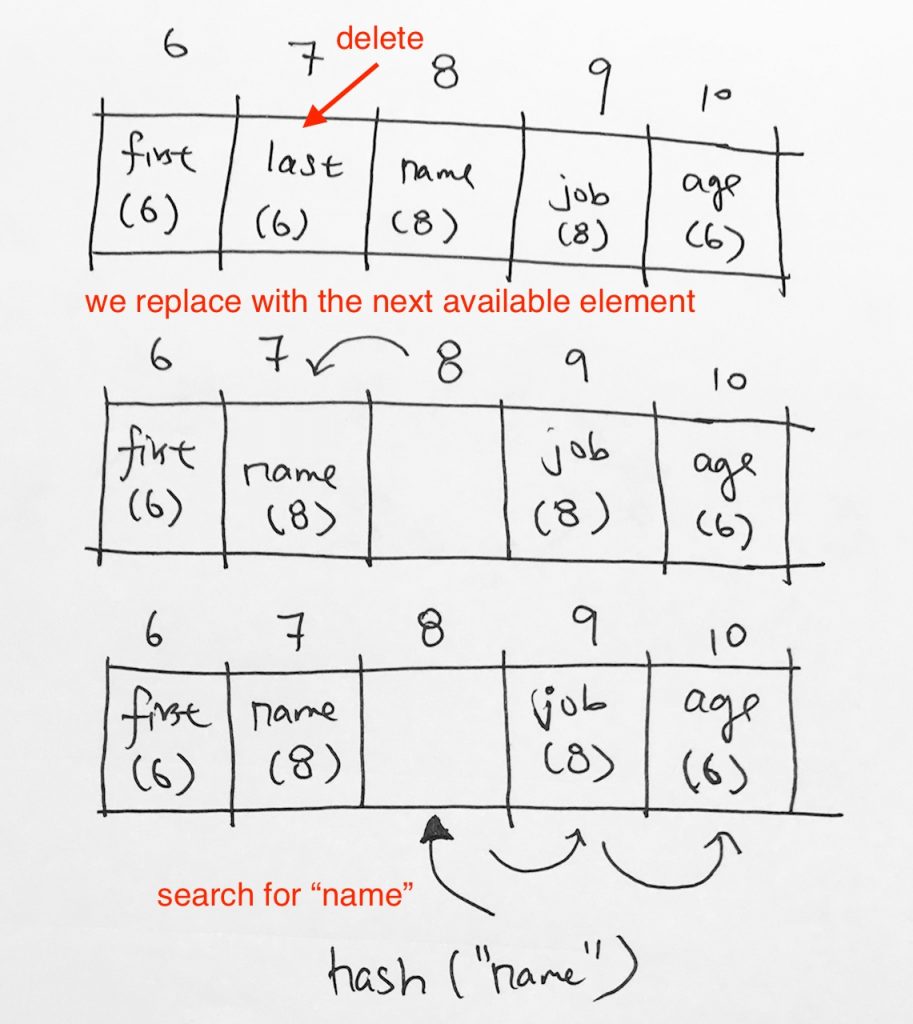
Sa we want to delete key “last”, which was initially hashed to index 6, and probed to index 7. Now, from the previous example, we know we can’t just let it go like this.
We must go down the line and find a replacement. The notion is that we must find a replacement that has key <= our key. But what if we dont' do this? What will happen? Say we simply get the next available replacement, which in our case, is key "name" (initially indexed to 8). So as you can see, say we bring key "name" over to index 7. Then, we make a search for key "name". Its initial hash index would be 8. And it wouldn't find anything there. If data does get placed there, it wouldn't be key "name" that we're looking for. Let's see what would happen if we iterated the array for a cell that has a key <= to our key. Picking an element with hash <= removed element's hash
So after removing key “last”, we can’t just get any element to replace it. We must find an element with a hash <= our hash. Since we’ve removed “last” with key of 6, we then iterate the array to find that element.
We go down the list, name has hash 8, nope. job has hash 8. nope. age has has 6. Perfect! so we move the element with key “age” and hash 6 to index 7. Don’t forget that we must do this continuously until we hit an empty slot or the end of the array.
Now, when you try to search for “age”, it will hash you to index 6, which you collide with key first. Then you probe. At index 7, we have found the element with key “age”. done!
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
this.delete = function(toDeleteKey) { let toDeleteIndex = this.retrieveIndex(toDeleteKey); if (!this.array[toDeleteIndex]) { console.log(`Sorry! this element does not exist`); return false; } let toDeleteHash = this.array[toDeleteIndex].hash; if (this.array[toDeleteIndex]) { // when a cell i is emptied this.array[toDeleteIndex] = null; // it is necessary to search forward through the following cells for (let i = toDeleteIndex+1; i < this.array.length; i++ ) { // of the table until finding either another empty cell // When an empty cell is found, then emptying cell i is // safe and the deletion process terminate if (!this.array[i]) { console.log(`cell ${i} is empty. We done`); return true; } else { // the cell is valid, so check its hash // if the hash is <= to toDelete hash, we can switch. if (this.array[i].hash <= toDeleteHash) { this.array[toDeleteIndex] = this.array[i]; toDeleteIndex = i; toDeleteHash = this.array[i].hash; this.array[i] = null; } } } // for console.log("didn't find anything"); } else console.log(`Sorry key does not exist`); } |
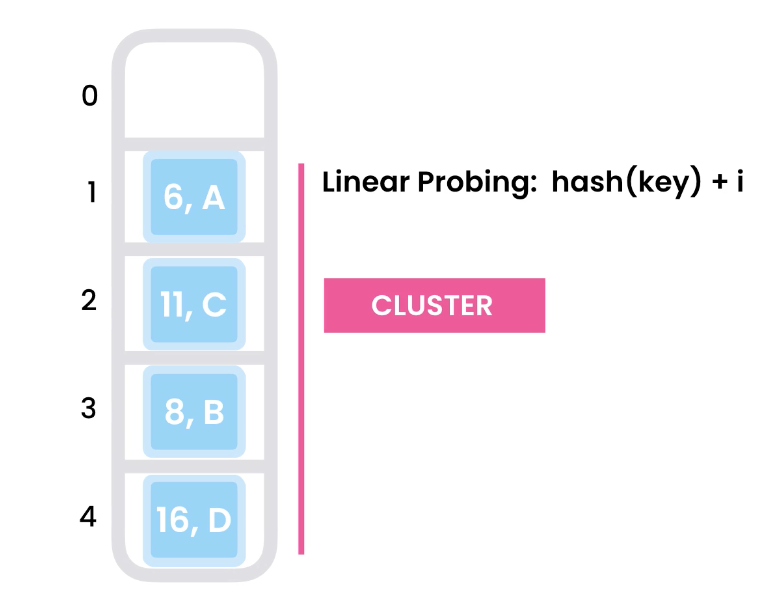
Problems of Linear probing – Cluster
Due to linear probing, clusters may form. Its when we keep hashing to an index and then linearly adding items down the line. A cluster will start forming at the hash index and future hashes will be unwieldy because every future hash will have to step through that cluster.
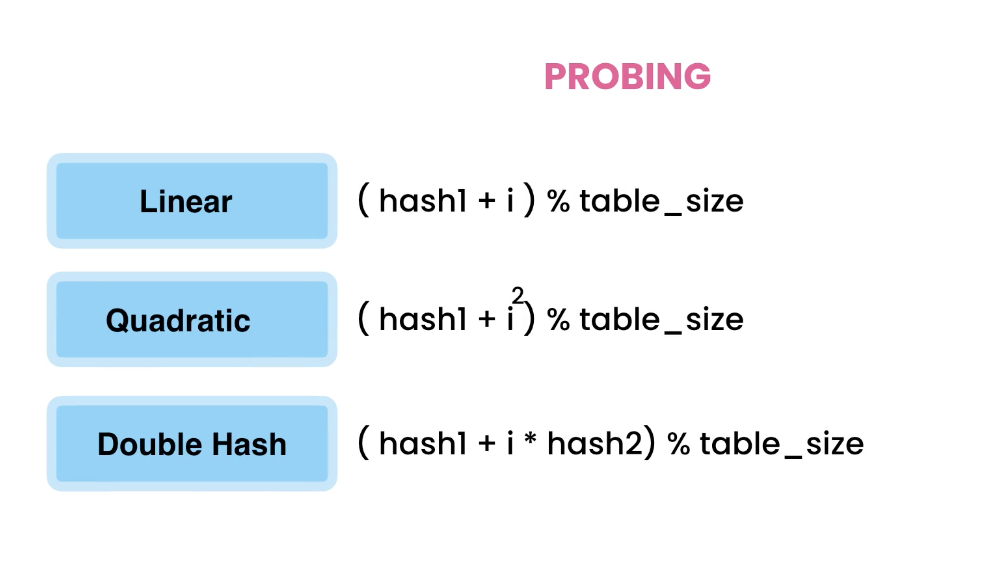
To solve this problem, we use Quadratic Probing.
((hash(key) + i)^2) % TABLE_SIZE
How will it prevent from probing?
With linear probing, we increase step by step. But if we step quadratically, our steps will widen, and this spread the insertions out.
However, the problem here is that Quadratic Probing will circle back and it keeps making the same jumps. This ends up with infinite loop.
Double Hashing
Given,
prime is a prime # smaller than TABLE_SIZE.
hashOne(key) = key % TABLE_SIZE,
hashTwo(key) = prime – (key%prime),
i as current index
DoubleHashing(key) = (hashOne(key) + i * hash2(key)) % TABLE_SIZE
Before, we used i for
Linear: i
Quadratic: i^2
now, we use Double: i * hash2