Heaps (Binary Tree, priority queues)

code – https://github.com/redmacdev1988/binaryHeap

Another type of Binary tree is the Heap.

A Heap is a binary tree that must have these two properties:

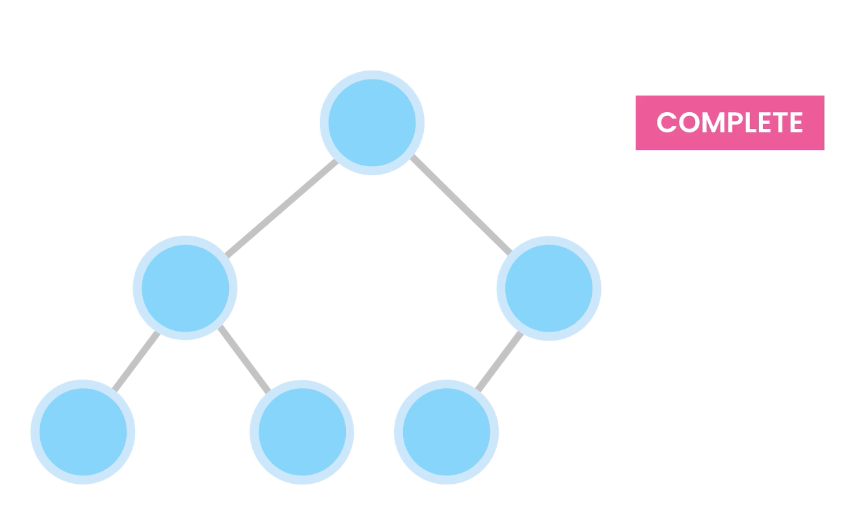
1) A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.

Also, nodes are inserted from the left to right.

For example, these are complete trees:

/ \

15 30

/ \ / \

40 50 100 40

/ \

15 30

/ \ / \

40 50 100 40

/ \ /

8 7 9

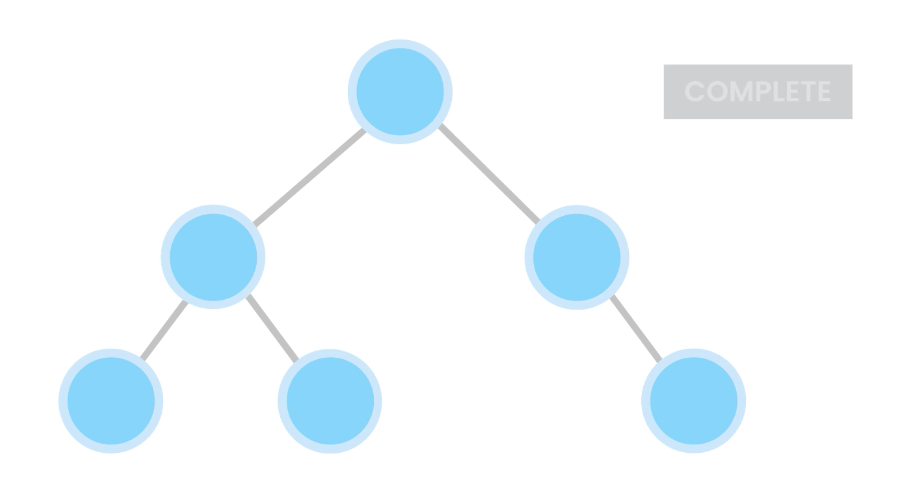
Not complete, because because one of the leafs has a hole in it.

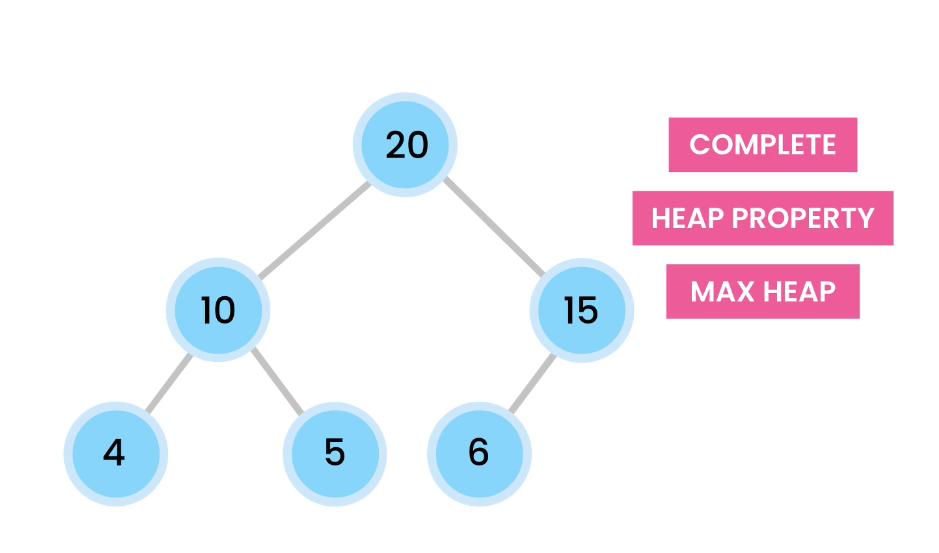
2) Heap property – The value of the parent node is greater than or equal to its children.

A heap is a complete binary tree that satisfies the heap property.

When the largest values start from the root, it’s called a max heap.

The opposite of that, is the min heap, where the smallest value is at the root.

Applications of Heaps

sorting (Heap sort)
graph algorithms (Shortest Path)
Priority Queues
Finding the k-th smallest or largest value

Operations of Heap

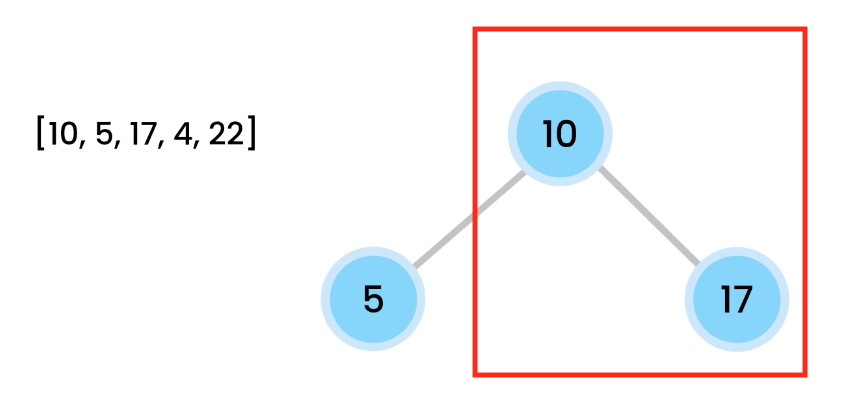
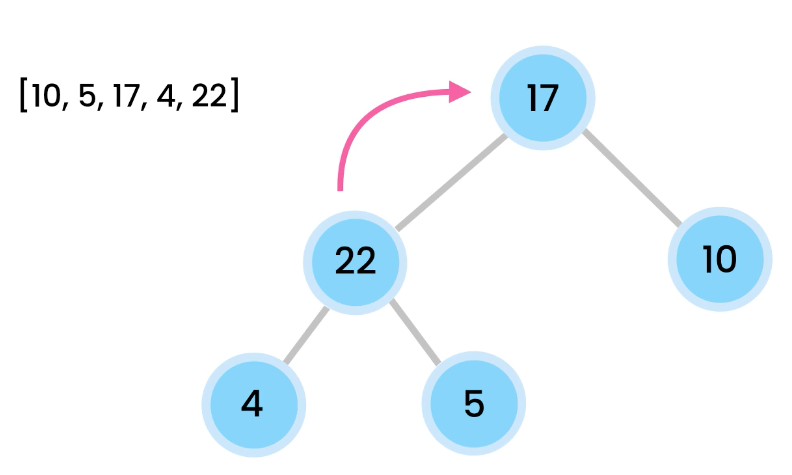
[10, 5, 17, 4, 2]

We add 10 the tree as the root.

Then add 5 from the left.

From left to right, we add, so we then add 17.

However, here 17 violates the max heap rule because parents should be larger or equal to children.

We then bubble the 17. We switch their positions and now 17 is at the root. 5 is on the left. 10 is on the right.

The heap (max heap example)

A max heap has the rule that the parent node must always have a higher priority than its child.

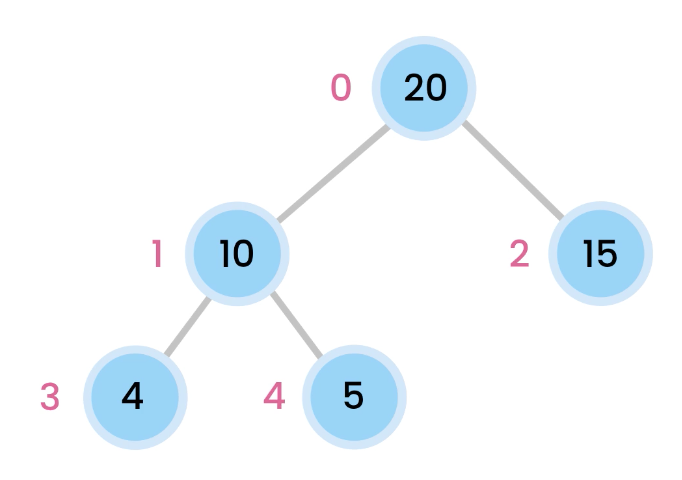
Each node is placed like a tree, however, take caution that there is no left/right references. Everything is accessed via index of the array. If we do want to access children of the node, its children will be indexed like so:

for the left child: 2x + 1
for the right child: 2x + 2

Inserting a node with a larger priority

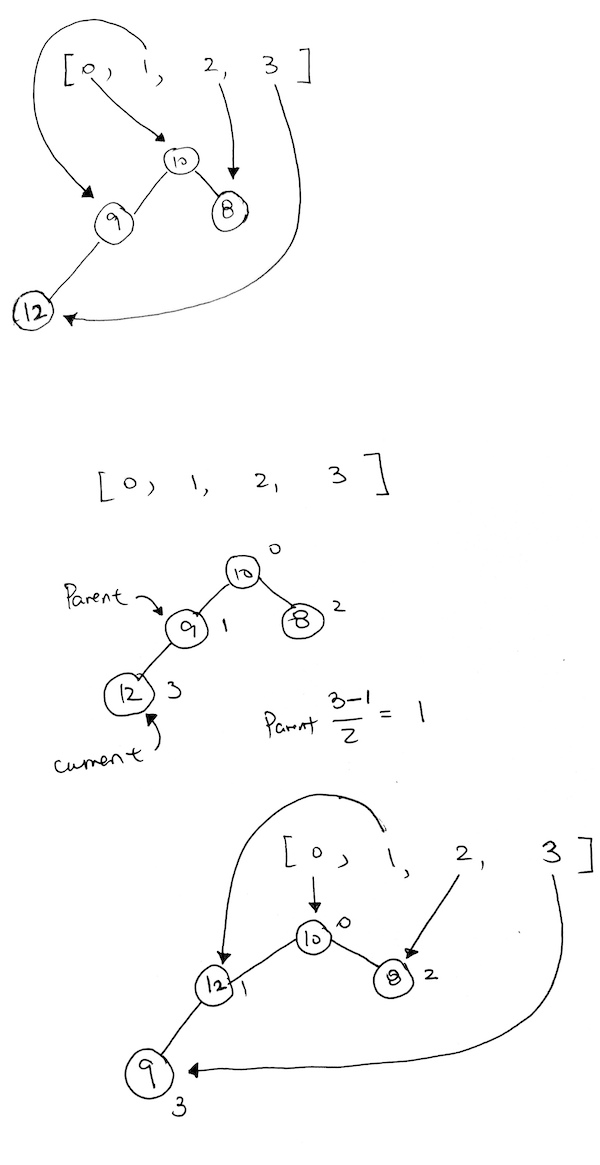
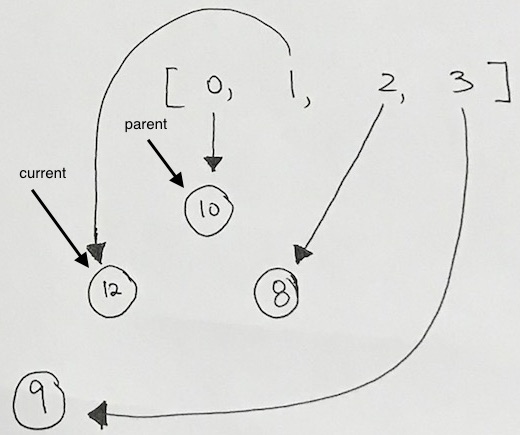
Let’s say we insert a node with a higher priority than its parent. In the example below, we try to insert 12. Obviously, 12 is larger than 8, and thus, we need to readjust.

First, we check to see if its parent (index 1) is valid. It is, so we have the array reference that WAS pointing to the parent, re-point to the the new node.

Then, have the array reference (with index 3) that was originally pointing to the new node, point to the parent.

We add 4, it satisfies heap property.

We then add 22. Oops, violation.

Then then swap 22 with 5. And then swap 22 with 17.

When largest values would bubble up.

The longest a value can travel is the height of the tree.
O(log n).

height = log(n).
O(log n).

In heaps, we can only delete the root node. And then fill it in with another value that maintains the heap property.

To do this, we move the last value on the heap (5) to the root. We fix the heap properties by bubbling 5 down and moving 17 up.
We pick larger child and swap.

Time complexity is O(log n) – removing value from heap
Finding max/min value is O(1) – root

Implementation

Store everything in array. Start from root, where index is 0.

left node’s index = parent node index * 2 + 1
right node’s index = parent node index * 2 + 2

index of parent of node = Math.floor((node’s index-1)/2)

Additional Material

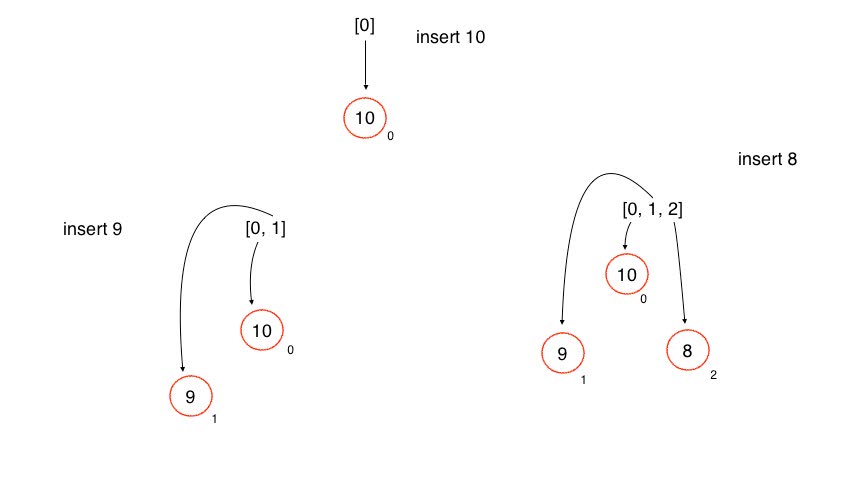
We have an array property in the constructor called heap. By definition, this array is contiguous memory, and can be indexed, starting from 0.

When we insert a node to the heap array, we allocate a new Node object in memory. Then the 0th index will contain a reference to that Node. When we insert the next node, another node will be allocated in memory, and we then have the 1st index reference that node.

Every node created will be inserted this way.

Thus, the latest current node will always have index heap.length – 1.

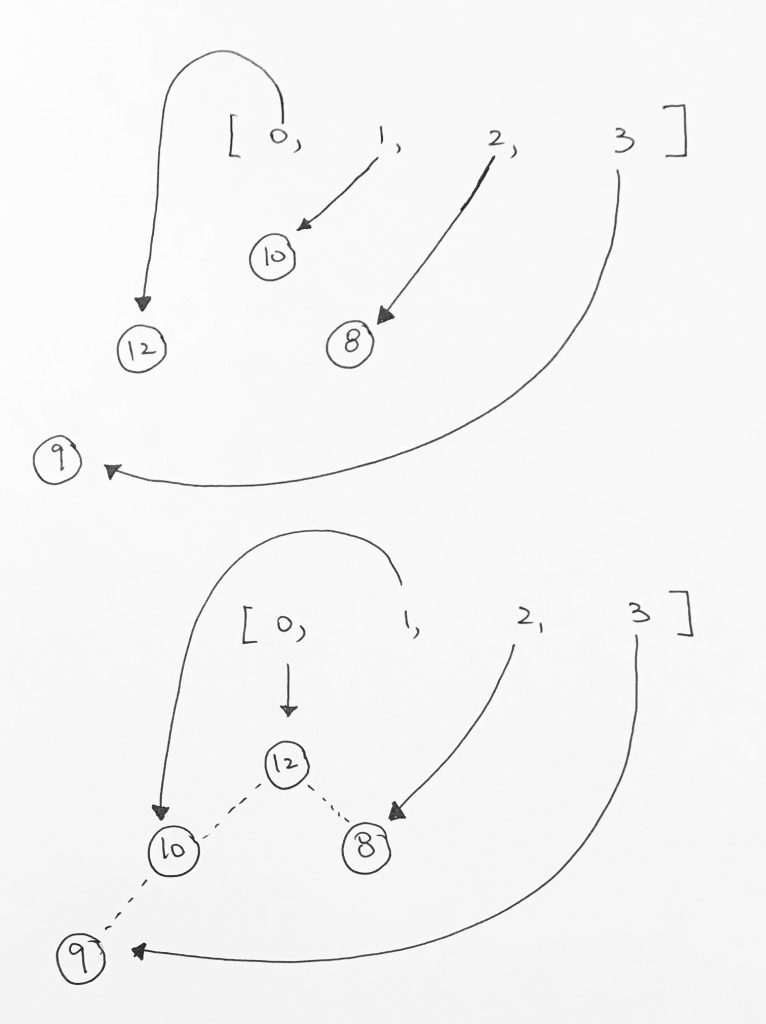
Then we add 12. However 12 violates the heap property.

Now, we recalculate the current node index and the parent node index. We want to move one level up so we can calculate index like so:

1 2	currentNodeIdx = currentNodeParentIdx; currentNodeParentIdx = Math.floor((currentNodeIdx-1)/2);

The easiest way for us to move up the tree is to simply have the current index take on the parent index. Then, recalculate the parent index via:

Math.floor((currentNodeIdx-1)/2)

As you see here, we have a violation. 12, being the child of 9, is larger than its parent. So we must bubble 12 up.

After the first bubble, we still have a violation because 12 is larger than its parent 10.
So now we just repeat what we did above.
Is the parent node valid? Yes.
Is the priority of the current node larger than the parent? Yes.

We then have the parent index’s reference point to the larger valued node. And have the current indexed element reference the smaller node. Our nodes gets reshuffled for ease of viewing, but the concept stands. Index 0 is now pointing to the node with the largest value. And all heap properties hold.

insertion code

Note that Math.floor(currentNodeIdx-1/2) is same as Math.ceil(currentNodeIdx-2/2). It gets the parent node’s index.

class Node {

constructor(val, priority) {

this.value = val;

this.priority = priority;

this.next = null;

}

class PriorityQueue {

constructor() {

this.heap = []; // array, with first null element

}

print(index) {

let next = 2 * index + 1;

console.log("***")

for (let v = 0; v < this.heap.length; v++) {

if (v === next) {

console.log("\n***");

// then recalculate

next = 2 * v + 1;

}

process.stdout.write(`${this.heap[v].value} | `);

}

// worse case, number of levels, translates to O(log n)

insert (value, priority) {

const newNode = new Node(value, priority);

this.heap.push(newNode);

console.log(`length - ${this.heap.length}`);

// assign node index to last element

let currentNodeIdx = this.heap.length-1;

// -1 means no parent

let currentNodeParentIdx = Math.floor((currentNodeIdx-1) / 2);

console.log(`last node index: ${currentNodeIdx},

parent index: ${currentNodeParentIdx}`);

// 1) if the parent node exist

// 2) the new node's priorioty is larger than the parent node priority

while(this.heap[currentNodeParentIdx] &&

newNode.priority > this.heap[currentNodeParentIdx].priority) {

// keep a reference to parent because we need it later

const parent = this.heap[currentNodeParentIdx];

// we access node by indexes.

this.heap[currentNodeParentIdx] = newNode;

this.heap[currentNodeIdx] = parent;

// recalculate indexes to move up the tree for

// the next checkup

currentNodeIdx = currentNodeParentIdx;

currentNodeParentIdx = Math.ceil((currentNodeIdx-2)/2);

}

let a = new PriorityQueue();

a.insert("Feed the kids", 10);

a.insert("feed the wife", 9);

a.insert("feed self", 5);

a.insert("feed the pets", 6);

a.print(0);

Heap Removal O( log n )

1) Removal means we pop the root node and process it.
2) Then we get the last element and copy it over to the root node.
3) Use top bottom to push it down if needed.

First, we copy the last value in the tree ( last element of the array ) onto the root. Then remove the last element, and decrease the heap size counter.

remove() {

let toProcess = this.heap[0];

console.log(`√ Processing task ${toProcess.value}`);

this.heap[0] = this.heap[this.heap.length-1];

this.heap.pop();

this.topToBottomHeapify(0);

}

From there we recursively push the root value down the tree so that it satisfies the heap property of where key(parent) >= key(child) if its max heap, and <= if its min heap. We decide on which child node to go down by comparing the two child nodes. We switch the parent value with the largest of the 2 child nodes.

topToBottomHeapify(currentIndex) {

let current = this.getCurrentNode(currentIndex);

if (!current) {return null;} else {

console.log(`processing index ${currentIndex} for value: ${this.heap[currentIndex].value}`);

}

let left = this.getLeftChild(currentIndex);

let right = this.getRightChild(currentIndex);

if (left && !right && left.priority > current.priority) {

this.exchangeCurrentAndLeftChild(currentIndex, left);

} else if (!left && right && right.priority > current.priority) {

this.exchangeCurrentAndRightChild(currentIndex, right);

} else if (left && right && (left.priority > current.priority || right.priority > current.priority)) {

console.log(`both left and right exists: ${left.priority}, ${right.priority}, and one of them is larger than parent`);

if (left.priority > right.priority) {

this.exchangeCurrentAndLeftChild(currentIndex, left);

} else {

this.exchangeCurrentAndRightChild(currentIndex, right);

}

this.topToBottomHeapify(2*currentIndex+1);

this.topToBottomHeapify(2*currentIndex+2);

}

Full Source Code

100

101

102

class Node {

constructor(val, priority) {

this.value = val;

this.priority = priority;

this.next = null;

}

class PriorityQueue {

constructor() {

this.heap = []; // array, with first null element

}

print(index) {

console.log("----- PRINTING HEAP --------")

let next = 2 * index + 1;

console.log("***")

for (let v = 0; v < this.heap.length; v++) {

if (v === next) {

console.log("\n***");

// then recalculate

next = 2 * v + 1;

}

process.stdout.write(`${this.heap[v].value}, ${this.heap[v].priority} | `);

}

console.log("\n--------- finished printing heap -----------");

}

// worse case, number of levels, translates to O(log n)

insert (value, priority) {

const newNode = new Node(value, priority);

this.heap.push(newNode);

let currentNodeIdx = this.heap.length-1;

let currentNodeParentIdx = Math.ceil( (currentNodeIdx-2) / 2);

while(this.heap[currentNodeParentIdx] &&

newNode.priority > this.heap[currentNodeParentIdx].priority) {

const parent = this.heap[currentNodeParentIdx];

this.heap[currentNodeParentIdx] = newNode;

this.heap[currentNodeIdx] = parent;

currentNodeIdx = currentNodeParentIdx;

currentNodeParentIdx = Math.ceil((currentNodeIdx-2)/2);

}

} // insert

getLeftChildIndex(currentIndex) {return 2 * currentIndex + 1;}

getRightChildIndex(currentIndex) {return 2 * currentIndex + 2;}

getLeftChild(currentIndex) {return this.heap[this.getLeftChildIndex(currentIndex)];}

setLeftChild(currentIndex, newNode) {this.heap[this.getLeftChildIndex(currentIndex)] = newNode;}

getRightChild(currentIndex) {return this.heap[this.getRightChildIndex(currentIndex)];}

setRightChild(currentIndex, newNode) { this.heap[this.getRightChildIndex(currentIndex)] = newNode;}

getCurrentNode(currentIndex) { return this.heap[currentIndex]; }

setCurrentNode(currentIndex, newNode) {this.heap[currentIndex] = newNode;}

exchangeCurrentAndLeftChild(currentIndex, left) {

let temp = this.getCurrentNode(currentIndex);

this.setCurrentNode(currentIndex, left);

this.setLeftChild(currentIndex, temp);

}

exchangeCurrentAndRightChild(currentIndex, right) {

let temp = this.getCurrentNode(currentIndex);

this.setCurrentNode(currentIndex, right);

this.setRightChild(currentIndex, temp);

}

topToBottomHeapify(currentIndex) {

let current = this.getCurrentNode(currentIndex);

if (!current) {return null;} else {

console.log(`processing index ${currentIndex} for value: ${this.heap[currentIndex].value}`);

}

let left = this.getLeftChild(currentIndex);

let right = this.getRightChild(currentIndex);

if (left && !right && left.priority > current.priority) {

this.exchangeCurrentAndLeftChild(currentIndex, left);

} else if (!left && right && right.priority > current.priority) {

this.exchangeCurrentAndRightChild(currentIndex, right);

} else if (left && right && (left.priority > current.priority || right.priority > current.priority)) {

console.log(`both left and right exists: ${left.priority}, ${right.priority}, and one of them is larger than parent`);

if (left.priority > right.priority) {

this.exchangeCurrentAndLeftChild(currentIndex, left);

} else {

this.exchangeCurrentAndRightChild(currentIndex, right);

}

this.topToBottomHeapify(2*currentIndex+1);

this.topToBottomHeapify(2*currentIndex+2);

}

remove() {

let toProcess = this.heap[0];

console.log(`√ Processing task ${toProcess.value}`);

this.heap[0] = this.heap[this.heap.length-1];

this.heap.pop();

this.topToBottomHeapify(0);

}

Tests

let a = new PriorityQueue();

a.insert("6680", 6680);

a.insert("8620", 8620);

a.insert("1115", 1115);

a.insert("7792", 7792);

a.insert("32895", 32895);

a.insert("51518", 51518);

a.insert("81187", 81187);

a.insert("1390", 1390);

a.print(0);