basic hash table to Strings (xcode 8.3.3)
Hash table with a stack or queue (xcode 8.3.3)
HashTable with choice for data structure
http://www.partow.net/programming/hashfunctions/
https://www.quora.com/Why-are-prime-numbers-used-for-constructing-hash-functions
http://algs4.cs.princeton.edu/34hash/
Why do hash functions use prime numbers?
https://cs.stackexchange.com/questions/11029/why-is-it-best-to-use-a-prime-number-as-a-mod-in-a-hashing-function
Why do hash functions use prime numbers for number of buckets ?
Consider a hash function (or a set of numeric data) that gives you multiples of 10.
If we use a bucket size of say, 4 buckets, we get:
10 mod 4 = 2
20 mod 4 = 0
30 mod 4 = 2
40 mod 4 = 0
50 mod 4 = 2
So from the set of hash results such as {10, 20, 30, 40, 50}, if we were to hash them into our buckets, all of them would go either into bucket 0, or bucket 2. all odd numbers would collide at bucket 2. All even numbers collide at bucket 0. The distribution of data into buckets is not good.
Let’s say we used 7 buckets instead. We take the generated hash keys, and do the mod to see how they are distributed throughout the hash table:
10 mod 7 = 3
20 mod 7 = 6
30 mod 7 = 2
40 mod 7 = 4
50 mod 7 = 1
much better. The numbers are getting distributed more evenly.
Let’s say we used 5 buckets.
10 mod 5 = 0
20 mod 5 = 0
30 mod 5 = 0
40 mod 5 = 0
50 mod 5 = 0
Even though 5 is a prime number, all of our keys are multiples of 5, and thus the mod will always be 0. This will distribute all of our keys into bucket 0.
Therefore, this means we have to choose a prime number that doesn’t divide our keys, choosing a large prime number is usually enough.
the reason prime numbers are used is to neutralize the effect of patterns in the keys in the distribution of collisions of a hash function.
In other words, say we have a function that generates a set (or just a simple data list) of data K
|
1 2 3 4 5 6 7 |
function generateList() { let array = []; for(let i = 0; i < 8888; i++) { array.push(rand()*(i+rand())); } return array; } |
Function generateList generates array: {0, 2, 3, 5, 6, 7, 9, 11, 12, 13, 14, 15, 18, 19, 24, 27, 28, 29, 30, 36, 42, 48 ….etc}
We use a hash table where the number of buckets is m = 12 (non-prime)
Let’s call each number inside of data K, a hash key. So 0 is a hash key. 1 is a hash key. 2 is a hash key. 5 is a hash key, and so on.
We map a hash key onto the bucket size m via AND 0xff, or % array size m. (In our example, we use % array size)
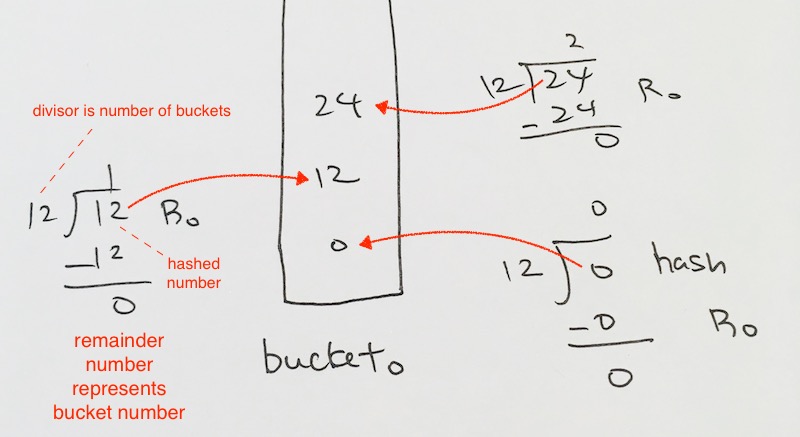
0 % 12 = 0
12 % 12 = 0
24 % 12 = 0
36 % 12 = 0
Thus, for every integer K in our list , 12, 24, 36…would all hash to bucket 0.
The other integers will have their respective buckets
2 % 12 = 2
3 % 12 = 3
…
…
13 % 12 = 1
14 % 12 = 2
15 % 12 = 3
18 % 12 = 6
19 % 12 = 7
…
Given, N is the number of buckets in a hash table. Let’s say 4.
If K is uniformly distributed, in other words, if K has integers (distribution) which has all outcomes equally likely, then the choice of bucket size ‘m’ is not so critical. For example, 1,2,3,4,5,6….etc, thus, K’s integer distribution all comes out equally likely.
However, there is an issue which can arise if the keys being hashed are not uniformly distributed. Specifically when the keys result in values in which N is a factor of that key, or the key is a multiple factor of N.
i.e.
4 is a factor of 20, 40, 60, 80. In the same way, 20 is a multiple factor of 4. 40 is a multiple factor of 4, and so on.
if K is 4, then K is a factor of N (4). 4 % 4 = 0
if K is 20, then K is a multiple factor of N(4). 20 % 4 = 0
4 is factor of 20, 20 % 4 = 0, key 20 get bucket 0
4 is factor of 40, 40 % 4 = 0, key 40 get bucket 0
4 is factor of 60, 60 % 4 = 0, key 60 get bucket 0
4 is factor of 80, 80 % 4 = 0, key 80 get bucket 0
In this situation, integer K, that aren’t factors of N or multiples of factors of N will remain empty, causing the load factor of the other buckets to increase disproportionately.
This situation seems to be the only valid reason to use a prime number. Given that a prime number has only itself and one as factors, using a prime number to resolve this problem means even if the keys are not uniformly distributed and instead possess some of kind structure (specifically multiples of a value), the likelihood that those values will arbitrarily hash to either the value one or N (the prime number) will be vanishingly small.
But, what happens if K is not uniformly distributed? Imagine that the keys that are most likely to occur are the multiples of 10 (like our example above) such as 10, 20, 30, 40, 50…and they keep appearing a lot.
In this case, all of the buckets that are NOT multiples of 10 will be empty with high probability (which is really bad in terms of hash table performance).
In general:
Every key in K (every integer in our array) that shares a common factor with the (number of buckets) m will be hashed to a bucket that is a multiple of this factor.
Every key in K, let’s say 14, which has factors 2, 7.
# of buckets (12) – 2, 3, 4, 6.
14 shares a common factor of 2 with (m, 12 buckets)
Hence any multiples of 14 will be hashed to a bucket that is a multiple of 2.
14 % 12 = 2
28 % 12 = 4
42 % 12 = 6
56 % 12 = 8
70 % 12 = 10
84 % 12 = 0
98 % 12 = 2
…
…
…
Hence, every key in K – 14, 28, 42, 56, …etc
that shares a common factor with (m number of buckets, 12) – common factor is 2
will be hashed to a bucket that is a multiple of that common factor (which is 2, 4, 6, 8)
Therefore, to minimize collisions, it is important to reduce the number of common factors between m and the elements of K. How can this be achieved?
By choosing m to be a number that has very few factors: a prime number.
extending String
initially getting an index from String is used like this:
|
1 2 3 4 5 6 |
let temp = String("hehe")! // get a string // use String.startIndex, and offset to select which character you want let result = temp.index(temp.startIndex, offsetBy: 1) print("\(temp[result])") |
We call String’s index, use its variable startIndex (which is a static String.Index)
to indicate we start at beginning of the String. Then we off set by i. And that’s where we’ll
return the character in the String.
|
1 2 3 4 5 6 7 |
extension String { subscript(i: Int) -> Character { let indexResult = index(startIndex, offsetBy: i) return self[indexResult] } } |
By using the subscript above, we simply use it to initialize a String, then return that String
|
1 2 3 4 5 |
extension String { subscript(i: Int) -> String { return String(self[i] as Character) } } |
Finally, in we extend Character, and create a var ASCII.
In it, we first create a String with its self Character. We access unicodeScalars, which is a
list of ASCII numbers for each character.
|
1 2 3 4 5 6 |
extension Character { var ASCII : Int { let s = String(self).unicodeScalars return Int(s[s.startIndex].value) } } |