Typescript
Part 1 – The split
Originally, we recurse into a function, along with a base case.
|
1 2 3 4 5 6 7 8 |
function recursion(index: number) : void { console.log(index); if (index <= 0) { return; } // (1) base case recursion(index-1); // (2) console.log(index); } recursion(3); |
Printing the parameter first will count down from 3.
When we hit our terminating case of zero at (1), we return, and execution from the recursion continues downwards at (2).
As each function pops off from the stack, we log the index again. This time we go 1, 2, and finally back to 3.
Thus display is:
3 2 1 0 1 2 3
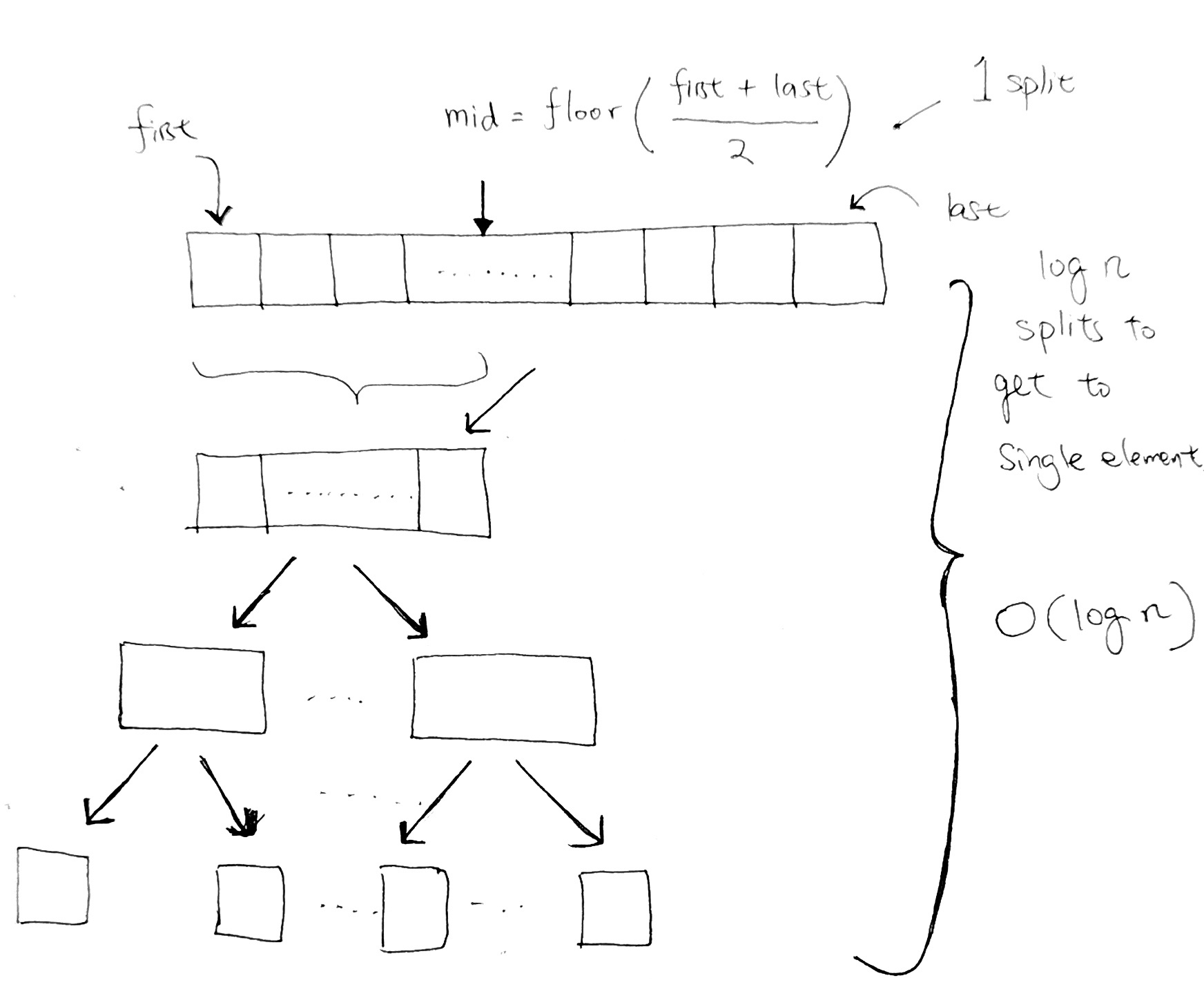
In Mergesort, the idea is that there is a total of n elements. We use splitting in half in order to cut down everything into single elements. Each cut is the same concept behind going down one level in a binary tree. We half all the elements.
In order to reach single elements, the running time is the height of the tree, or (log n) splits.
And in order to go into each halved section to split some more, we use recursion.
Let’s look at how MergeSort does this split:
in code:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
type StrOrNumArr = number [] | string []; class MergeSort { private _data: StrOrNumArr; constructor(arr: StrOrNumArr = null) { this._data = arr ? arr : ["haha", "hoho", "hehe", "hihi", "alloy", "Zoy"]; } private split(start: number, end: number) { if (start >= end) { // Reached single element, stop the recursion console.log(this._data[start]); // print it return; } const mid = Math.floor((start+end)/2); this.split(start, mid); this.split(mid+1, end); } public run() { this.split(0, this._data.length-1); } } const test = new MergeSort(); test.run(); |
The output is:
haha, hoho, hehe, hihi, alloy, Zoy
Part 2 – The Merge
Printing the words out is our first step, and we’ve used recursion. Now we need to compare each word and sort everything.
When we get to haha, we return an array with “haha”. Same with “hoho”. As we recursive back down the stack one step, we now have two arrays. We need to compare everything in these two arrays and sort them into a new array.
- We first create a n space ‘result’ array that is the total length of the arrays.
- We do this so that we will sort each element of these two arrays and put them into our result array.
- We do this until one of the arrays finish.
- Then we just tack on whatever is left from the array that still has untouched elements
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 |
const _left = ["a", "x"]; const _right = ["c", "m", "r", "z"]; function merge(leftArr, rightArr) : StrOrNumArr { let resultIndex = 0; const resultArr = new Array(leftArr.length + rightArr.length); let leftIndex = 0; let rightIndex = 0; while ((leftIndex <= leftArr.length - 1) && (rightIndex <= rightArr.length - 1)) { const leftElement = leftArr[leftIndex]; const rightElement = rightArr[rightIndex]; if (leftElement < rightElement) { resultArr[resultIndex++] = leftElement; leftIndex++; } if (rightElement < leftElement) { resultArr[resultIndex++] = rightElement; rightIndex++; } } // leftover at left array if (leftIndex < leftArr.length) { while (leftIndex < leftArr.length) { resultArr[resultIndex++] = leftArr[leftIndex++]; } } // leftover at left array if (rightIndex < rightArr.length) { while (rightIndex < rightArr.length) { resultArr[resultIndex++] = rightArr[rightIndex++]; } } console.log('result', resultArr); return resultArr; } merge(_left, _right); |
Full code
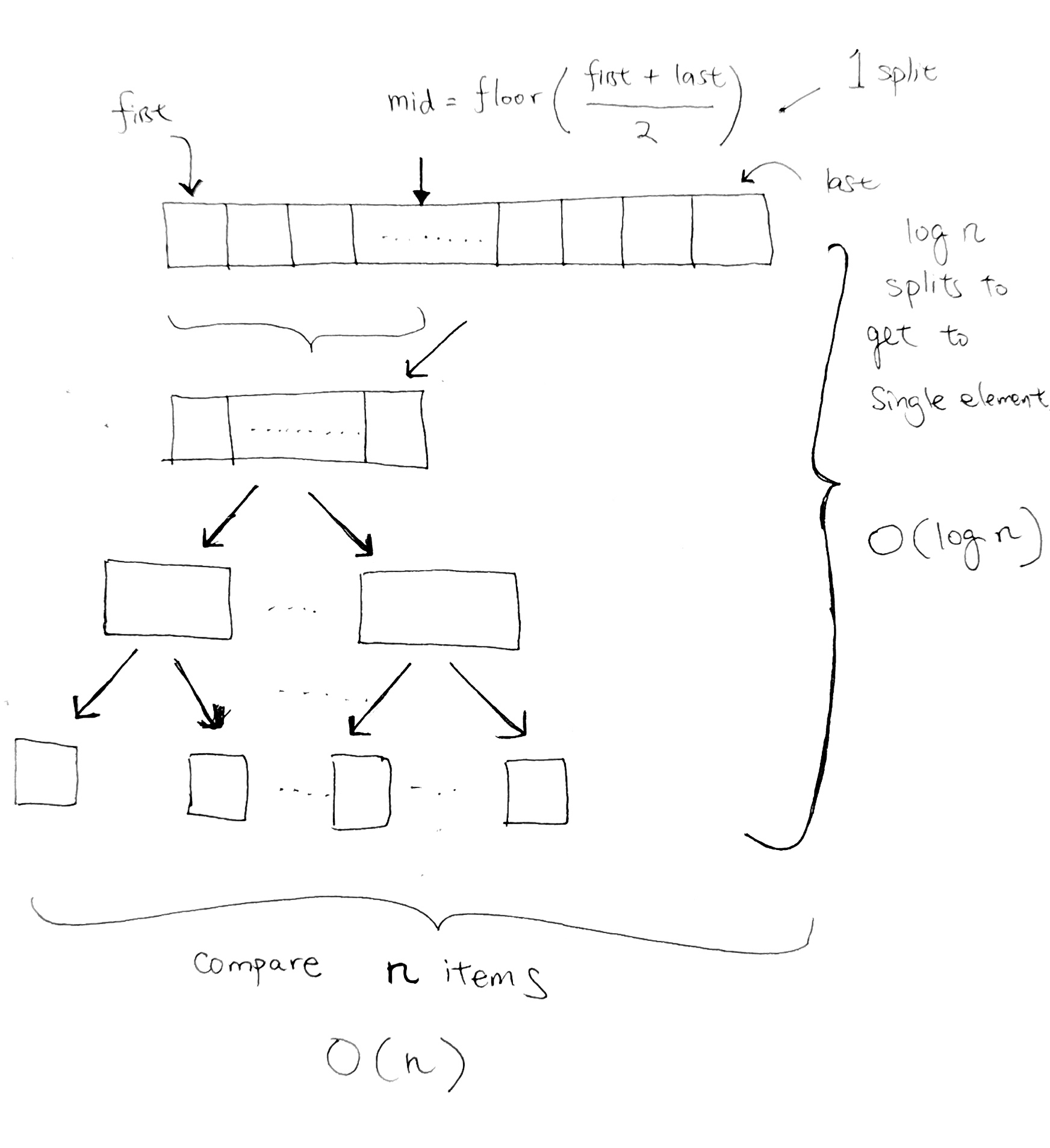
Each level represents one split. And we have a total of (log n) split.
At every level, we do a comparison for every element. Thus our running time for the sort is O(n log n).
The standard merge sort on an array is not an in-place algorithm, since it requires O(N) additional space to perform the merge. During merge, we create a result array in order to carry the left and right array. This is where O(n) additional space comes from:
|
1 |
const resultArr = new Array(leftArr.length + rightArr.length); |
However, there exists variants which offer lower additional space requirement.
It is stable because it keeps the ordering intact from the input array.
Say we have [‘a’, ‘a’, ‘x’, ‘z’]. We split until we get single elements.
[‘a’, ‘a’] and [‘x’, ‘z’]
[‘a’] [‘a’] [‘x’] [‘z’]
We compare ‘a’ and ‘a’.
|
1 2 3 4 5 6 |
if (rightElement === leftElement) { resultArr[resultIndex++] = leftElement; resultArr[resultIndex++] = rightElement; leftIndex++; rightIndex++; } |
This is where it is stable because we always keep the 1st ‘a’ before the 2nd ‘a’ in the results array, which requires O(n) Auxiliary space, during the merge.
We place the leftmost ‘a’ first. Then we put the right side ‘a’ next into the result array.
Say we have another sample data where [‘a’, ‘z’, ‘m’,’b’, ‘a’, ‘c’] and we start recursing via mid splits:
[‘a’, ‘z’, ‘m’] [‘b’, ‘a’, ‘c’]
[‘a’, ‘z’] [‘m’] [‘b’, ‘a’] [‘c’]
[‘a’] [‘z’] [‘m’] [‘b’] [‘a’] [‘c’]
Now we star the merge process:
[‘a’, ‘z’] [‘m’] [‘a’, ‘b’] [‘c’]
[‘a’, ‘m’, ‘z’] [‘a’, ‘b’, ‘c’]
As you can see at this part, we do the final merge and because ‘a’ === ‘a’, we always insert the left-side ‘a’ inside of our results array first. Then we place the right-side ‘a’. Thus, keeping it stable.
Full Source (Typescript)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 |
type StrOrNumArr = number [] | string []; class MergeSort { private _data: StrOrNumArr; public _chops: number; constructor(arr: StrOrNumArr = null) { this._data = arr ? arr : ["haha", "hoho", "hehe", "hihi", "alloy", "Zoy", "ABC", "you know me", 'michael', 'Jackson']; } // O(n) - linear time to merge private merge(leftArr, rightArr) : StrOrNumArr { let resultIndex = 0; // auxiliary space O(n) const resultArr = new Array(leftArr.length + rightArr.length); let leftIndex = 0; let rightIndex = 0; while ((leftIndex <= leftArr.length - 1) && (rightIndex <= rightArr.length - 1)) { const leftElement = leftArr[leftIndex]; const rightElement = rightArr[rightIndex]; if (leftElement < rightElement) { resultArr[resultIndex++] = leftElement; leftIndex++; } if (rightElement < leftElement) { resultArr[resultIndex++] = rightElement; rightIndex++; } if (rightElement === leftElement) { resultArr[resultIndex++] = leftElement; resultArr[resultIndex++] = rightElement; leftIndex++; rightIndex++; } } // leftover at left array if (leftIndex < leftArr.length) { while (leftIndex < leftArr.length) { resultArr[resultIndex++] = leftArr[leftIndex++]; } } // leftover at left array if (rightIndex < rightArr.length) { while (rightIndex < rightArr.length) { resultArr[resultIndex++] = rightArr[rightIndex++]; } } return resultArr; } private split(start: number, end: number) { if (start >= end) { // base cancel recursion case console.log(this._data[start]); return [this._data[start]]; } const mid = Math.floor((start+end)/2); const leftArr = this.split(start, mid); const rightArr = this.split(mid+1, end); return this.merge(leftArr, rightArr); } public run() { console.log('running MergeSort algorithm'); const result = this.split(0, this._data.length-1); console.log('result', result); } } const test = new MergeSort(); test.run(); |
Javascript version
In-Place: The standard merge sort on an array is not an in-place algorithm, since it requires O(N) additional space to perform the merge. There exists variants which offer lower additional space requirement.
Stable: yes. It keeps the ordering intact from the input array.
http://www.codenlearn.com/2011/10/simple-merge-sort.html
Merge Sort has 2 main parts. The 1st part is the double recursion. The 2nd part is the Merge itself.
1) double recursion
2 recursion calls is executed, one after the other. Usually, in a single recursion, we draw a stack with the recursion and its parameter, and calculate it that way.
However, with two recursions, we simply have more content on the stack in our drawing.
For example, say we have an array of integers, with index 0 to 10.
mergeSort says:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
private void mergeSort(int[] array, int left, int right) { if (left < right) { //split the array into 2 int center = (left + right) / 2; //sort the left and right array mergeSort(array, left, center); mergeSort(array, center + 1, right); //merge the result merge(array, left, center + 1, right); } } |
So we call mergeSort recursively twice, with different parameters. The way to cleanly calculate them is to
write out the parameters, see if the left < right condition holds. If it does, then write result for the 'center' variable.
Evaluate the 2 mergeSort calls and the merge Call. You will then clearly see the order of execution:
Let’s take a look at how the cursive call operates
Say we have [‘a’, ‘b’, ‘c’, ‘d’, ‘e’]
So we first operate on partition(0, 4).
start = 0, end = 4
[‘a’, ‘b’, ‘c’, ‘d’, ‘e’]
We try to find the floor mid point index:
(0+4)/2 = 2, mid value is ‘c’
Now we have:
partition(0, 2) or partition([‘a’, ‘b’, ‘c’])
partition(3,4) or partition([‘d’, ‘e’])
Let’s work on the first one:
partition([‘a’, ‘b’, ‘c’])
floor mid point is (0+2)/2 = 1 [0, 1] mid value is ‘b’
Now we have:
partition(0, 1) or partition([‘a’, ‘b’])
partition(2,2) or partition([‘c’])
We try to find mid point index:
(0+1)/2 = floor (0.5) = 0
Now we have:
partition(0, 0) or partition([‘a’]) returns ‘a’
partition(1, 1) or partition([‘b’]). returns ‘b’
going up the recursion, partition([‘c’]) returns c.
Great.. so now we have values a, b, c. and finished [‘a’, ‘b’, ‘c’] at the top.
Now we need to process
partition([‘d’, ‘e’])
find mid point index (3+4)/2 = floor(3.5) = 3.
So we get
partition(3,3) returns ‘d’
and partition(4,4) returns ‘e’
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
export default class MergeSort { private arr: string []; private start: number = 0; private end: number = 0; constructor(strArr: string []) { this.arr = strArr; this.end = this.arr.length - 1; } private partition(start: number, end: number) { console.log(`start ${start}, end ${end}`) if (start < end) { const floorMid = Math.floor((start+end)/2); console.log(`floorMid - ${floorMid} ${this.arr[floorMid]}`); this.partition(start, floorMid); this.partition(floorMid+1, end); } if (start >= end) { console.log(`[end] - ${start} ${this.arr[start]}`); } } public run() { debugger this.partition(this.start, this.end); } } |
2) The merging itself
The merging itself is quite easy.
- Use a while loop, and compare the elements of both arrays IFF the cur for both arrays have not reached the end.
- Whichever is smaller, goes into the result array.
- Copy over leftover elements from the left array.
- Copy over leftover elements from the right array.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
private void merge(int[] array, int leftArrayBegin, int rightArrayBegin, int rightArrayEnd) { int leftArrayEnd = rightArrayBegin - 1; int numElements = rightArrayEnd - leftArrayBegin + 1; int[] resultArray = new int[numElements]; int resultArrayBegin = 0; // Find the smallest element in both these array and add it to the result // array i.e you may have a array of the form [1,5] [2,4] // We need to sort the above as [1,2,4,5] while (leftArrayBegin <= leftArrayEnd && rightArrayBegin <= rightArrayEnd) { if (array[leftArrayBegin] <= array[rightArrayBegin]) { resultArray[resultArrayBegin++] = array[leftArrayBegin++]; } else { resultArray[resultArrayBegin++] = array[rightArrayBegin++]; } } // After the main loop completed we may have few more elements in // left array copy them. while (leftArrayBegin <= leftArrayEnd) { resultArray[resultArrayBegin++] = array[leftArrayBegin++]; } // After the main loop completed we may have few more elements in // right array copy. while (rightArrayBegin <= rightArrayEnd) { resultArray[resultArrayBegin++] = array[rightArrayBegin++]; } // Copy resultArray back to the main array for (int i = numElements - 1; i >= 0; i--, rightArrayEnd--) { array[rightArrayEnd] = resultArray[i]; } } |
Running Time
Running time for the double recursion
Average and Worst time:
O(n log n)
How?
The log n comes from the fact that merge sort is recursive in a binary way.
4 items, takes 2 divisions to get to the base items.
8 items, takes 3 divisions to get to the base items.
…if you keep going like this, you’ll see that its logarithmic in nature.
Running time for the merge
We are dividing the array along the recursive path.
So length n1 and n2 keeps changing and the complexity of merge routine/method at each call.
It is ‘n’ on the first call to recursion (leftArray of size n/2 and rightArray of size n/2)
It is ‘n/2’ on the second call to recursion. (we merge two n/4 arrays)
It is ‘n/4’ on the third call to recursion. (we merge two n/8 arrays)
……. and so on …..
till we merge just 2 items ( leftArray of size 1 and rightArray of size 1) and base case there is just one item, so no need to merge.
As you can see the first call to recursion is the only time the entire array is merged together at each level, a total of ‘n’ operations take place in the merge routine.
Hence that is why its O( n log n )