ref – https://www.tutorialspoint.com/Dijkstra-s-algorithm-in-Javascript

Dijkstra’s Algorithm is used for solving single source shortest path problems. In this algorithm, a single node is fixed as a source node and shortest paths from this node to all other nodes in graph is found.

Minimum priority queue is the most commonly used data structure for implementing Dijkstra’s Algorithm because the required operations to be performed in Dijkstra’s Algorithm match with specialty of a minimum priority queue.

Time complexity of Dijkstra’s algorithm is O(N2) because of the use of doubly nested for loops. It depends on how the table is manipulated.

Dijkstra’s Algorithm cannot be applied on graphs having negative weight function because calculation of cost to reach a destination node from the source node becomes complex.

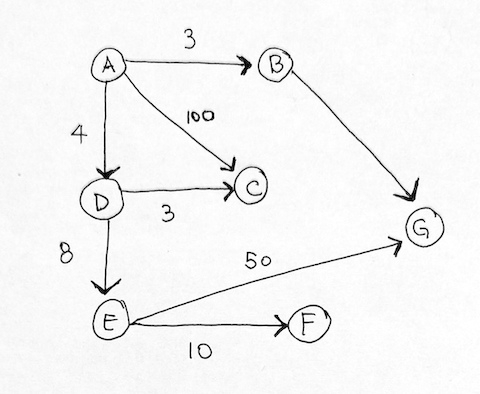
Given nodes: A B C D E F G
and their edges:

“A”, “C”, 100
“A”, “B”, 3
“A”, “D”, 4
“D”, “C”, 3
“D”, “E”, 8
“E”, “F”, 10
“B”, “G”, 9
“E”, “G”, 50

We first draw a node graph diagram of it. Keep in mind that from our adjacency list, if we have arrows pointing to each other from two nodes, it’s undirected. If it’s only from one to the other, then it’s directed. So undirected graphs should have double the # of edges than directed graphs.

In our case, it is a directed graph.

Then we set up the the node/distance/prev chart.
The distance means the shortest distance from the starting node to that node. Right now, we initialize all to infinity.
The prev means the previous node that this node connects to. We maximize as null.

Since our starting node is A, our distance is 0, and prev is A.

node	distance	prev
A	0	A
B	Inf	null
C	Inf	null
D	Inf	null
E	Inf	null
F	Inf	null
G	Inf	null

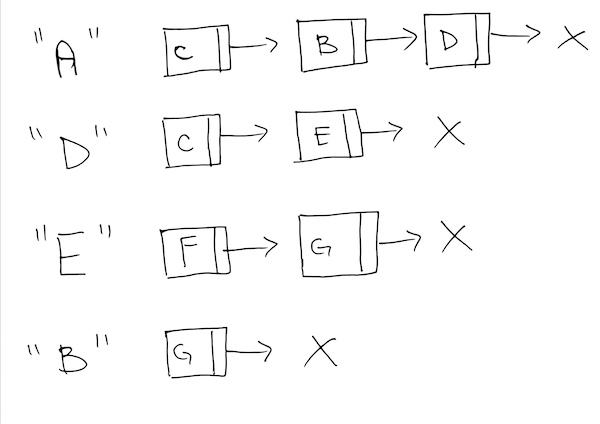
We then draw the adjacency graph to keep track of all the neighbors of a specific node presented from edges.
For each edge, it creates a neighbor of a node, and we must diagram this in order to keep track.

Finally, we have a queue to get the minimum distance as shall see later.

Start

In our code, we create an instance of our Dijkstra’s Algorithm.

We have the queue ready, so we first push A onto the queue.
queue – [A]

We start by popping the A off the queue and processing it.
queue – []

We look at the unvisited neighbors of A.
Namely, they are C, B, and D.

Distance from A to C is 100. On our chart, distance of A to C is Infinity. 100 < Infinity, so we replace Infinity with 100. Then we push C onto the queue. queue - [C]

node	distance	prev
A	0	A
B	Inf	null
C	100	A
…

Distance from A to B is 3. On the chart, A to B’s distance is Infinity. Is 3 < Infinity? Yes! so we replace the values in the chart, then push node B onto the queue: queue - [B, C]

node	distance	prev
A	0	A
B	3	A
C	100	null
…

Distance from A to D is 4. On the chart A to D’s distance is Infinity. Is 4 < Infinity? Yes! so we replace it on the chart, and push node D onto the queue: queue - [B, D, C]

node	distance	prev
A	0	A
B	3	A
C	100	A
D	4	A

We’ve processed all of node A’s neighbors. (Linked List) Once that’s done. The queue is a priority minimum queue, so we pop the queue to get the minimum distanced node, which is B.

Queue – [D, C]

B with priority of 3

At B, we process all its unvisited neighbors. In the Adjacency list, B is connected to G. B to G is 9. Distance from starting point A to B is 3.
so 3 + 9 = 12. Is 12 < Infinity? yes, so let's update the table.

node	distance	prev
A	0	A
B	3	A
C	100	A
D	4	A
…
G	12	B

Then we push G onto the queue.

Queue – [D, G, C]

Processing D, priority 4

But because D has the minimum distance at 4, we pop it from the queue.

Queue – [G, C]

D has edges to C and E.

Distance from D to C is 3. Distance from start to D 4. Distance from start to C = 3 + 4 = 7. Is 7 < Infinity? Yes, let's update it. Insert C with priority 7 into the queue. Notice we already have priority 100 for C in the queue. We simply replace the value 100 with 7. This is so because we have found a shorter distance than 100.

node	distance	prev
A	0	A
B	3	A
C	7	D
D	4	A
…
G	12	B

We then look at neighbor E. From D to E is 8. From start to D is 4. From start to E is 4 + 8 = 12. Is 12 < Infinity ? Yes, update table. Then push E with priority 12 onto the queue.

node	distance	prev
A	0	A
B	3	A
C	7	D
D	4	A
E	12	D
…
G	12	B

so we’re finished running through all edges for ‘D’.

Queue – [C(7), E(12), G(12)]

Process C with priority of 7

We pop C because it has minimum prioirty.

Queue – [E(12), G(12)]

C has no edges in our Adjacency list, so we skip.

Process G with priority of 12

Queue – [E(12)]

Then we process G with priority of 12. G has no edges in our Adjacency list, so we skip.

Process E with priority of 12

So we then process node E. It has edges F and G.

E to F is 10. Min distance from from start point A to E is 12.
Is 10+12=22 smaller than what’s on our chart? (Infinity) Yes! So we update the chart.

node	distance	prev
A	0	A
B	3	A
C	7	D
D	4	A
E	12	D
F	22	E
G	12	B

Then push F onto the queue.

Queue – [F(22)].

Let’s continue and process G.

E to G is 50. Minimum distance from start to E is 12.
Start to G is 50 + 12 = 62. From our Chart, A to G has 12. Is 62 < 12? No! So we don't update the chart. We do not push G onto the queue. We then pop the queue and continue...

Processing F at priority 22

No edges for F. Queue is empty. WE’re now done.

The final answer is:

node	distance	prev
A	0	A
B	3	A
C	7	D
D	4	A
E	12	D
F	22	E
G	12	B

Where the shortest distance from A to any of the nodes are listed under the distance column.

For example, say I want to know what is the shortest distance from A to G. It is 12 by the way of A, B, G. The 12 shows that A to G takes 12 steps and G’s previous is B. We look at B and its previous is A. So we know that it goes A -> B -> G.

I want to know what is the shortest distance from A to C. Looking at the chart, A to C has min distance of 7, by the way of A, B, C.
C’s previous is B. And B’s previous is A.

Code Explanation

So we have a bunch of dictionaries to represent our chart data. We have everything from distance, prev, and nodes. We have _edges to represent the adjacency list, and _visited to show which ones have been visited.

let _nodes = [];

let distanceArr = {};

let prevArr = {};

let _edges = {};

let _visited = {};

We set up a minimum priority queue.

1	let pq = new PriorityQueue();

And initialize everything first. The start node’s distance is always 0.
We set the other distances to Infinity.
We set the previous nodes to null.
And finally, push the start node onto the queue.

distanceArr[startNode] = 0;

_nodes.forEach(node => {

if (node !== startNode)

distanceArr[node] = Infinity;

prevArr[node] = null;

});

pq.insert(startNode, 0);

So the basic idea here is that we start the algorithm by dequeueing the starting node.
We continue dequeueing from the priority queue until it is empty.

The point of processing each node as they come in is that we get the minimum priority (distance) first.
Then as we process them, we update the chart. We are done when the queue is empty.

let next = pq.remove();

while(next) {

// process the ledges of each node as they come off of the queue

next = pq.remove();

}

As each node with the minimum priority (distance) comes off the queue, we process their edge list. This can be visually seen by the adjacency list. In our case, it is the _edges dictionary.

let currValue = next.value;

// all neighbors of our node

let anEdge = _edges[currValue];

if (!_visited[anEdge.value]) {

let alt = distanceArr[currValue] + anEdge.priority;

if (alt < distanceArr[anEdge.value]) {

// update chart values

// enqueue this node since it has shorter distance

queue.insert(anEdge.value, distanceArr[anEdge.value]);

}

So if an edge has not been visited, we process it.
We the get the minimum distance from starting to current node, and then add the distance of the current edge.
If it’s less than what we have in the chart, we update the chart.

This is to say that we found a shorter way. In this case, we push the current node into the queue along with its distance as the priority.
Due to the queue being a minimum priority queue, it will always process the shortest distance nodes.

If it’s not, then this way is longer, and we don’t care for it.

Source Code

Node, Linked List and Minimum Priority Queue

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

141

142

143

144

145

146

147

148

149

150

151

152

153

154

155

156

157

158

159

160

161

162

163

class Node {

constructor(val, priority) {

this.value = val;

this.priority = priority;

this.next = null;

}

print() {

console.log(`${this.value} (${this.priority})`);

}

let createLinkedListInstance = (function LinkedList() {

let head = null;

let tail = null;

let iterator = null;

return new class LinkedList {

add = function(value, priority) {

if (!head && !tail) {

head = new Node(value, priority, null);

tail = head;

iterator = head;

} else {

tail.next = new Node(value, priority, null);

tail = tail.next;

}

print = () => {

console.log(`--- printing Linked List ---`);

for (let tmp = head; tmp != null; tmp = tmp.next) {

console.log(tmp);

}

next = () => {

if (iterator) {

let tmp = iterator;

iterator = iterator.next;

return tmp;

} else {

return null;

}

hasNext = () => { return iterator ? true : false; }

resetIterator = () => { iterator = head; }

}

});

class PriorityQueue {

constructor() {

this.heap = []; // array, with first null element

}

print(index) {

console.log("----- PRINTING HEAP --------")

//let next = 2 * index + 1;

//console.log("***")

for (let v = 0; v < this.heap.length; v++) {

//if (v === next) {

//console.log("\n***");

// then recalculate

//next = 2 * v + 1;

//}

//process.stdout.write(`${this.heap[v].value}, ${this.heap[v].priority} | `);

console.log(`${this.heap[v].value}, ${this.heap[v].priority} | `);

}

console.log("\n--------- finished printing heap -----------");

}

// worse case, number of levels, translates to O(log n)

insert (value, priority) {

const newNode = new Node(value, priority);

this.heap.push(newNode);

let currentNodeIdx = this.heap.length-1;

let currentNodeParentIdx = Math.ceil( (currentNodeIdx-2) / 2);

while(this.heap[currentNodeParentIdx] &&

newNode.priority < this.heap[currentNodeParentIdx].priority) {

const parent = this.heap[currentNodeParentIdx];

this.heap[currentNodeParentIdx] = newNode;

this.heap[currentNodeIdx] = parent;

currentNodeIdx = currentNodeParentIdx;

currentNodeParentIdx = Math.ceil((currentNodeIdx-2)/2);

}

} // insert

getLeftChildIndex(currentIndex) {return 2 * currentIndex + 1;}

getRightChildIndex(currentIndex) {return 2 * currentIndex + 2;}

getLeftChild(currentIndex) {return this.heap[this.getLeftChildIndex(currentIndex)];}

setLeftChild(currentIndex, newNode) {this.heap[this.getLeftChildIndex(currentIndex)] = newNode;}

getRightChild(currentIndex) {return this.heap[this.getRightChildIndex(currentIndex)];}

setRightChild(currentIndex, newNode) { this.heap[this.getRightChildIndex(currentIndex)] = newNode;}

getCurrentNode(currentIndex) { return this.heap[currentIndex]; }

setCurrentNode(currentIndex, newNode) {this.heap[currentIndex] = newNode;}

exchangeCurrentAndLeftChild(currentIndex, left) {

let temp = this.getCurrentNode(currentIndex);

this.setCurrentNode(currentIndex, left);

this.setLeftChild(currentIndex, temp);

}

exchangeCurrentAndRightChild(currentIndex, right) {

let temp = this.getCurrentNode(currentIndex);

this.setCurrentNode(currentIndex, right);

this.setRightChild(currentIndex, temp);

}

topToBottomHeapify(currentIndex) {

let current = this.getCurrentNode(currentIndex);

if (!current) {return null;} else {

console.log(`processing index ${currentIndex} for value: ${this.heap[currentIndex].value}`);

}

let left = this.getLeftChild(currentIndex);

let right = this.getRightChild(currentIndex);

if (left && !right && left.priority < current.priority) {

this.exchangeCurrentAndLeftChild(currentIndex, left);

} else if (!left && right && right.priority < current.priority) {

this.exchangeCurrentAndRightChild(currentIndex, right);

} else if (left && right && (left.priority < current.priority || right.priority < current.priority)) {

console.log(`both left and right exists: ${left.priority}, ${right.priority}, and one of them is larger than parent`);

if (left.priority < right.priority) {

this.exchangeCurrentAndLeftChild(currentIndex, left);

} else {

this.exchangeCurrentAndRightChild(currentIndex, right);

}

this.topToBottomHeapify(2*currentIndex+1);

this.topToBottomHeapify(2*currentIndex+2);

}

remove() {

let toProcess = this.heap[0];

if (toProcess) {

console.log(`√ Processing task ${toProcess.value}`);

this.heap[0] = this.heap[this.heap.length-1];

this.heap.pop();

this.topToBottomHeapify(0);

return toProcess;

} else {

console.log('now empty');

return null;

}

export { Node };

export { PriorityQueue };

export { createLinkedListInstance };

Dijkstra’s Algorithm

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

141

let l = console.log;

let DijkstraAlgo = (function() {

let _edges = {};

let _nodes = [];

let _visited = {};

return new class dijkstra {

constructor() {}

addNode = value => { _nodes.push(value); }

addDirectedEdge = (fromValue, toValue, priority) => {

let list = _edges[fromValue];

if (!list) {

_edges[fromValue] = createLinkedListInstance();

_edges[fromValue].add(toValue, priority);

} else { // neighbors exist

_edges[fromValue].add(toValue, priority);

}

dijkstraAlgorithm(startNode) {

let distanceArr = {};

let prevArr = {};

let pq = new PriorityQueue();

distanceArr[startNode] = 0;

pq.insert(startNode, 0);

_nodes.forEach(node => {

if (node !== startNode)

distanceArr[node] = Infinity;

prevArr[node] = null;

});

l(_nodes);

l(distanceArr);

l(prevArr);

let next = pq.remove();

while(next) {

let currValue = next.value;

console.log(`------------------- processing LIST of ${currValue} via priority ${next.priority}------------------`);

// all neighbors of our node

let edges = _edges[currValue];

if (edges) {

edges.print();

while (edges.hasNext()) {

let anEdge = edges.next();

if (!_visited[anEdge.value]) {

console.log(`neighbor name ${anEdge.value}, priority of neighbor ${anEdge.priority}, dist from ${currValue} to start point ${distanceArr[currValue]}`);

let alt = distanceArr[currValue] + anEdge.priority;

console.log(`distance from starting ${startNode} to ${anEdge.value} is ${alt}`);

console.log(`Is ${alt} < ${distanceArr[anEdge.value]} ?`)

// value is smaller than what's on the board

if (alt < distanceArr[anEdge.value]) {

// update our board so it has shorter value

distanceArr[anEdge.value] = alt;

// update the prev so we know which is the previous node

prevArr[anEdge.value] = currValue;

// insert all edges into our priority queue

// we put distance as priority so that smallest priority

// gets processed first

console.log(`Yes, insert ${anEdge.value} with priority ${distanceArr[anEdge.value]} into queue`)

pq.insert(anEdge.value, distanceArr[anEdge.value]);

}

_visited[currValue] = true;

l(distanceArr);

l(prevArr);

} else {

console.log(`No edges nodes for node ${currValue}`);

}

next = pq.remove();

console.log('==================================================');

}

l(distanceArr);

}

print = () => {

l(_nodes);

for (var key in _edges) {

if (Object.prototype.hasOwnProperty.call(_edges, key)) {

// do stuff

console.log('printing for key: ' + key);

_edges[key].print();

}

});

let g = new DijkstraAlgo();

g.addNode("A");

g.addNode("B");

g.addNode("C");

g.addNode("D");

g.addNode("E");

g.addNode("F");

g.addNode("G");

g.addDirectedEdge("A", "C", 100);

g.addDirectedEdge("A", "B", 3);

g.addDirectedEdge("A", "D", 4);

g.addDirectedEdge("D", "C", 3);

g.addDirectedEdge("D", "E", 8);

g.addDirectedEdge("E", "F", 10);

g.addDirectedEdge("B", "G", 9);

g.addDirectedEdge("E", "G", 50);

g.dijkstraAlgorithm("A");