A permutation is an act of arranging members in a set in all possible orders.

For example, for 1 2 3:

1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

A total of 6 combinations.

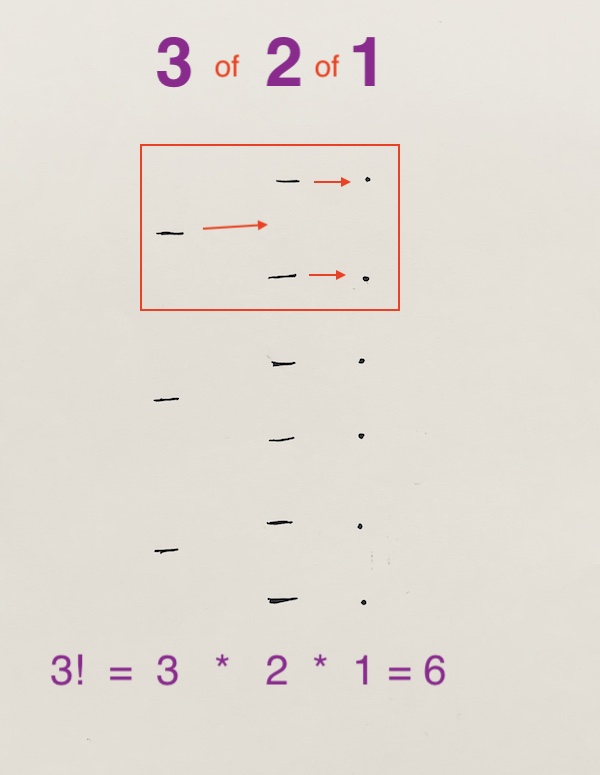
Mathmetically it is denoted as 3! = 3 * 2 * 1.

This means that if I had 3 things, There are 3 of 2 of 1 way in which I can arrange them.

Mathematically we’d say 3! = 3 * 2 * 1 = 6 permutations
4! = 4 * 3 * 2 * 1 = 24 permutations
…etc

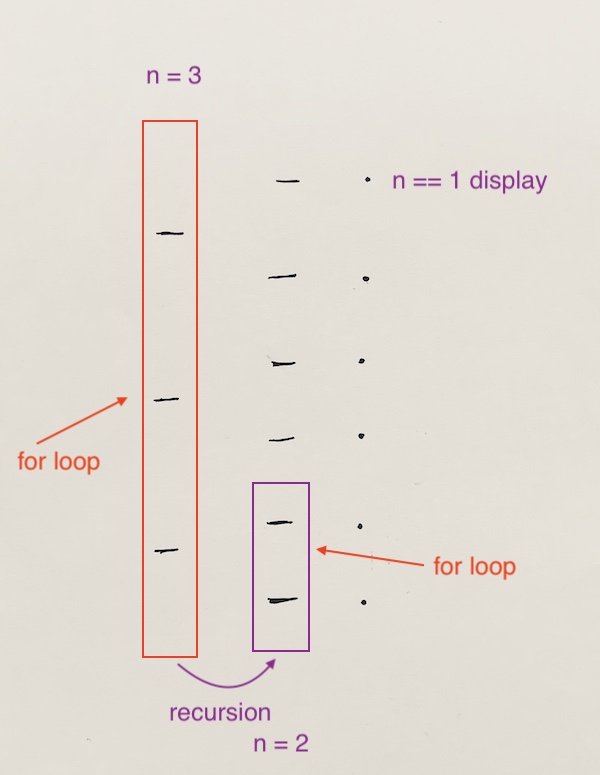
In order to put this permutation into code, each column is a for-loop.
When we process the next recursion, we subtract 1 from n, we call recursion( n – 1 ).

In other words:

At n = 3, which is column 3, there are three ticks. We loop through each of them.

For each index of the 3rd column, we call recursion with n – 1.

This brings us to n = 2, at the 2nd column. There are two ticks. We loop through them and call recursion with n – 1 for each of those ticks.

The recursion brings us to n = 1, at column 1. We display whatever is there.

If you were to run through it all, you’d log 6 times.

Hence what we’re essentially doing is 3 * 2 * 1 = 6 combination.