source code – https://github.com/redmacdev1988/boyerMoore/blob/master/index.js

The idea of prefix and suffix borders

A border is a substring which is both proper suffix and proper prefix.

For example, in string ‘ccacc’,’cc’ is a border because it appears in both end of string but ‘cca’ is not a border.

In string, ‘cacc’, ‘c’ is a border because it appears in both end of the string. ‘ca’ is not a border.

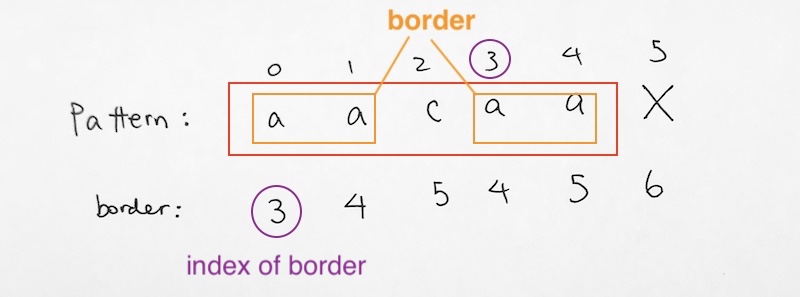
Let’s look at example where our pattern is aacaa, and an already calculated Suffix Border Index array.

At pattern index 0, we have string aacaa. Its border is aa.
Hence, the prefix border is ‘aa’ at [0][1].
The suffix border is ‘aa’ at [3][4].

We write the beginning index of the suffix border (3) into our border array at index 0.

Thus, for the border array at index 0, we write 3. This means that for the string at pattern index 0, the suffix border starts at index 3.

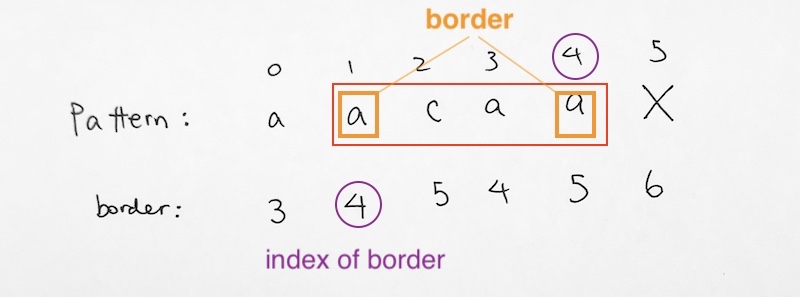
Let’s move on to pattern index 1. We have string acaa. The prefix border is ‘a’ at index 1. The suffix border ‘a’ at index 4.
Hence, for the border array at index 1, we write 4. This means that for the string at pattern index 1, the suffix border starts at index 4.

At pattern index 2, we have string ‘caa’. There is no border string. Thus, for the value in our border array, we simply write 5, which represents DNE.

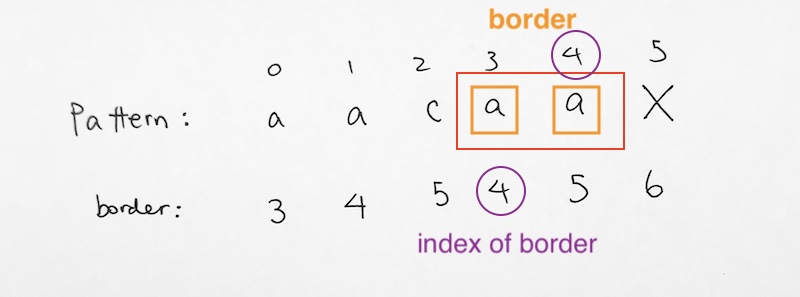
At pattern index 3, we have ‘aa’. The prefix border is ‘a’ at pattern index 3. The suffix border is ‘a’ at pattern index 4. This means that for the string at pattern index 3, the suffix border starts at index 4.

Finally, we come to the last character of pattern index 4 ‘a’. It is only 1 character and does not have any border. So we simply assign the length of the pattern to represent DNE.

How to calculate the Suffix Border Index table

1) to start off, we get the length of the pattern. This value will represent DNE for all the pattern substrings that do not have borders.

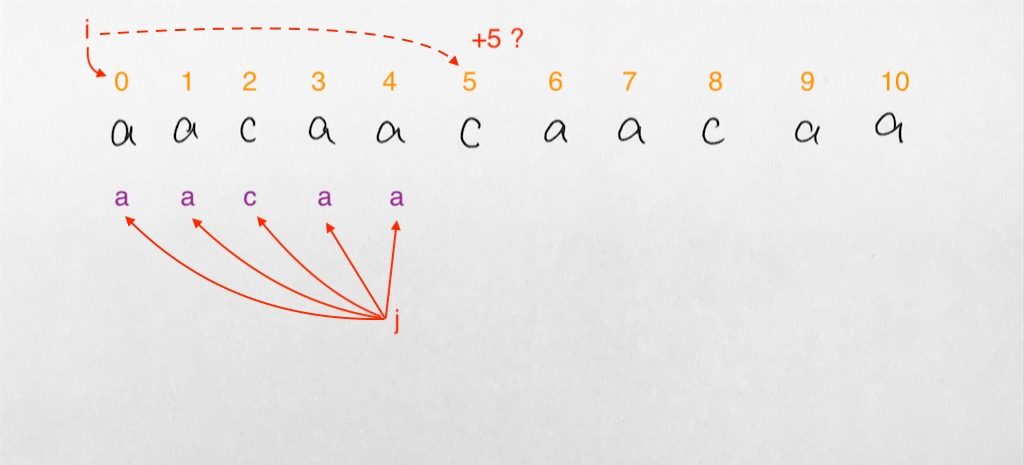
2) The idea is that we process it going backwards using two indexes i and j.
We simply have i go backwards. For each i iteration, we get index j and process it to check if the character at i and character at j matches.

3) If it matches, we record a suffix border index. If it doesn’t match, we simply assign it as length of the pattern to designate the suffix index DNE.

• i is index of the pattern substring.
• j is index of the suffix border.
• _borderPosition represents an array that contains all suffix border positions

Let’s look at it in detail:

Given pattern ‘aacaa’.

i = 5, j = 6.
border position for 5 is 6, because index 5 does not exist.

0 1 2 3 4 5 (index)
a a c a a X (pattern)
0 0 0 0 0 6 (suffix border index)

We then start going backwards for index i.

i is 5, j is 6

(5 > 0) √
(6 <= 5) X

our j index of 6 is larger than pattern length, so we skip.
decrement i, j to 4, 5.

_borderPosition[4] = 5. This means at pattern index 4, the border index is 5, which denotes DNE. It means the substring at pattern index 4 does not have a border.

0 1 2 3 4 5 (index)
a a c a a X (pattern)
0 0 0 0 5 6 (suffix border index)

i is 4, j is 5

(4 > 0) √
(5 <= 5) √

p[4-1] “a”
p[5-1] “a”

There’s a match so we don’t process index j anymore. We jump out of the loop and decrement i, j to 3, 4.

_borderPosition[3] = 4. This means at pattern index 3, which is substring ‘aa’, the suffix border index is 4.

0 1 2 3 4 5 (index)
a a c a a X (pattern)
0 0 0 4 5 6 (suffix border index)

i is 3, j is 4

(3 > 0) √
(4 <= 5) √

p[3-1] “c”
p[4-1] “a”

There’s no match so we keep processing index j.
We keep processing by going backwards on the _borderPosition array.

j = _borderPosition[4] = 5.

(3 > 0) √
(5 <= 5) √

p[3-1] “c”
p[5-1] “a”

j = _borderPosition[5] = 6.

(3 > 0) √
(6 <= 5) X

skip out of inner while loop
i–; j–; so i is now 2, j is now 5.
_borderPosition[2] = 5.

0 1 2 3 4 5 (index)
a a c a a X (pattern)
0 0 5 4 5 6 (suffix border index)

The substring ‘caa’ at index 2, does not have a suffix border index. So we give is value 5 to denote DNE.

i is 2, j is 5

(2 > 0) √
(5 <= 5) √

Notice j starts over again from the end. The reason we do this is so that we try to find borders. We go back to trying to see if there’s a match for “a”.
if there is, then the current index i has a prefix border.

p[2-1] “a”
p[5-1] “a”

i–;j–‘ 1, 4
_borderPosition[1] = 4;

0 1 2 3 4 5 (index)
a a c a a X (pattern)
0 4 5 4 5 6 (suffix border index)

We then go back one more step to see if there’s additional matches. For every match that happens, we record in the border position of that
match at j.

i is 1, j is 4

(1 > 0) √
(4 <= 5) √

p[1-1] = “a”
p[4-1] = “a”

_borderPosition[0] = 3

0 1 2 3 4 5 (index)
a a c a a X (pattern)
3 4 5 4 5 6 (suffix border index)

Why do we need Suffix borders?

Naive algorithm jumps 1 step at a time. But this is too slow.
Other ways, we jump pattern.length at a time. But we will miss out on potential matches in the middle.

Thus the suffix border array is created so we know where the potential matches are in the middle. WE calculate the suffix border so that we can jump to the correct prefix border for the next potential match.

Setting up the Shift array with Suffix Index Array

So given _borderPositions array as

0 1 2 3 4 5 (index)
a a c a a X (pattern)
3 4 5 4 5 6 (suffix border index)

This means that at index 0 of the pattern, 3 is the index in which the suffix border happens.

Given that if our shift array value is 0, this means it was not assigned.
In this case, we give it the default of the first value of the _borderPositions.

This is so that when we find a match, We know how many steps to skip down. For example, in our case, when a successful search is found, we always skip 3 steps (_shift[0] which is the _borderPosition[0]).

This is so that we can successfully start at the index of the next potential match.

After processing, our shift array looks like this:

0 1 2 3 4 index
3 3 3 3 1 shift

What this means is that while trying match our pattern char to the text char, if for any reason from index 0 to index 3 is a mismatch, we want our i to shift down 3 spaces. This is because 3 spaces down, there is potential for our pattern to match again due to the suffix border.

However, at index 4, if there’s a mismatch, we only shift i down 1. This is because our very first character is a mismatch so we always need to check for the next one. Also, in our shift array, _shift[4+1] is DNE, so we just use default step 1.

If say, our first character at index 4, matches, then index 3 is a mismatch, we shift i down text array 1 steps because _shift[3+1] = 1.

You can see it with an example like this:

0 1 2 3 4 5 6
b a a c a a b (text)
a a c a a (pattern)

we have a mismatch at index 3 because text[3] “c” != pattern[3] “a”.
Hence we take _shift[j+1] = _shift[4] = 1.

After we shift 1, we get

0 1 2 3 4 5 6
b a a c a a b (text)
_ a a c a a (pattern)

match!

The Search

We do the match going backwards:

• i is the index we’re going to use for every substring of the text
• j is the index on the pattern. We use this to compare the pattern char to the text char

if the chars at i and j keeps matching, we continue down until j is -1. This means we have matched every character in the pattern matched up in the text.

Thus, when j < 0, we found a pattern match in text. We then log i in order to let the user know where the match happens. Now, we move i down for the next substring to check for a match. So the issue here is, how many steps do we move i down? Typically, we would say, hey why not just shift the i down 5 steps because that's the length of our pattern. We've compared our pattern already, so its safe to go down 5 steps right? The answer is no. What we need to do is shift down 3 steps to the to _shift[0]. This is the 1st of the suffix border index. We need to do this in order to find substring potential matches.